Biais Positionnels dans les transformers auto-régressifs

Description du biais positionnel dans les transformers auto-régressifs

Introduction sur le biais positionnel

Le biais positionnel : c’est quoi ?

Le papier [Lost in the Middle: How Language Models Use Long Contexts](https://arxiv.org/pdf/2307.03172) décrit comment, pour des contextes très longs, les LLMs se concentrent surtout sur les débuts et la fin du prompt. Le biais positionnel dans les LLMs, c'est la tendance du modèle à se concentrer excessivement sur certaines parties de l'entrée, qu'importe la sémantique. Et cette concentration influence significativement les performances et la fiabilité des transformers: en fonction de l'ordre des éléments dans le prompt, le modèle va générer des réponses différentes. Notamment, plus on a un contexte long, plus le modèle a tendance à se concentrer sur les éléments au début et à la fin du prompt (effet "lost in the middle").

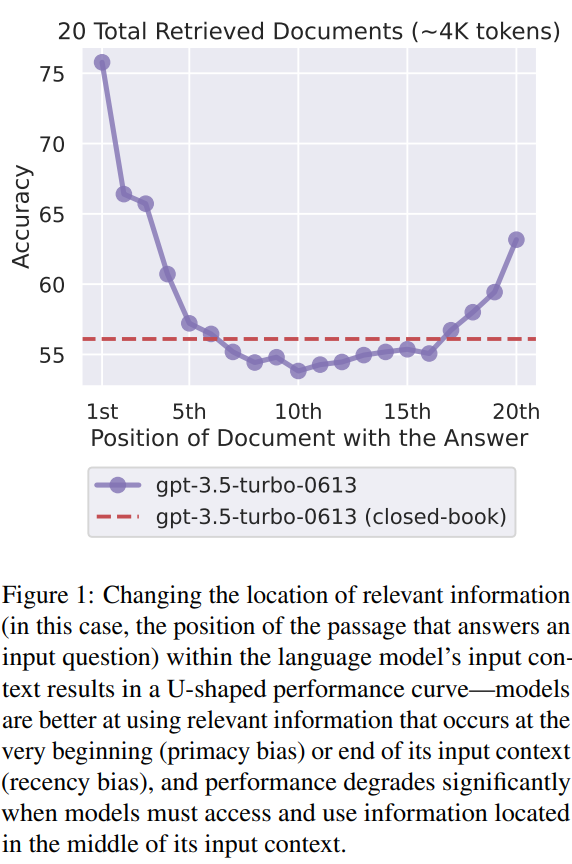
Le biais positionnel : ça vient d’où ?

• Le masque causal

  Avec un masque causal, chaque token ne peut voir que les tokens qui le précèdent. Cela signifie que les tokens situés au début sont accessibles à presque tous les calculs d’attention ultérieurs, alors que ceux situés plus tard ne le sont qu’à partir d’un certain point.

• L’encodage de position (relatif, RoPE…)

  Ce type d’encodage de position favorisent la proximité avec le token courant. Ainsi, les jetons situés près de la fin de la séquence bénéficient d’une attention renforcée, car leur représentation est plus fortement influencée par la similarité de position avec le token en cours de génération.

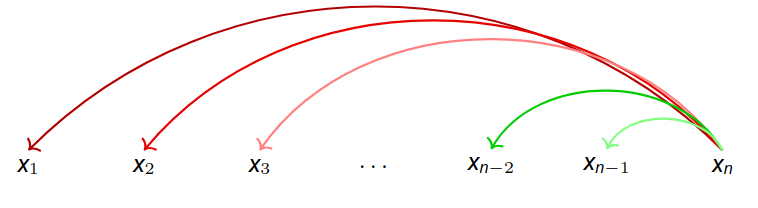
Qu’est-ce que l’encodage de position ?

L’encodage de position est nécessaire dans les transformers à cause du calcul de l’attention qui prend en compte tous les azutres tokens de la séquence. Sans encodage positionnel, chaque token identique aurait la même influence, peu importe l’endroit dans la séquence :
“Le chat mange la souris” et “La souris mange le chat” seraient équivalents. Avec l’encodage de position, deux tokens identiques mais à des positions différentes auront des vecteurs différents.

1. Encodage absolu (sinusoïdal ou appris)
   Ajouté aux embeddings initiaux. Limité pour extrapoler à des longueurs supérieures à celles vues à l’entraînement.

2. Encodages relatifs
   • T5 : biais appris pour chaque distance relative.
   • Alibi : biais fonctionnel selon la distance.
3. RoPE (Rotary Positional Encoding)
   rotation appliqué à la représentation intermédiaire de chaque token dépendante de la position du token au niveau du calcul du score d’attention (chaque paire de dimensions du vecteur est tournée dans le plan d’un angle qui dépend de sa position dans la séquence). Mais du coup, quand on applique cette rotation à query et key, et qu’on fait un produit scalaire, le dot product dépend de la position relative $i−j$, même si on encode chaque position de manière absolue.

SOTA des approches pour corriger le biais positionnel

1. Modifier le mécanisme d’attention

• Stable Mask (2402.04779)
  Ajout d’un “pseudo-score” $-\gamma\times(j-1)$ présente une approche de “compensation” du score d’attention excessif sur les premiers tokens en ajoutant un “pseudo-score”: $-\gamma \times (j-1)$ pour la j-ième position, qui diminue au fur et à mesure de la séquence.

• Calibration du score d’attention (2406.16008) présente une approche dans laquelle on a le score d’attention de la query avec un doc à la position k qui est fonction ($f$) de la pertinence du doc \(\text{rel}(\text{doc}_k)\) et du biais positionnel à la position k $b_k$. En simplifiant la fonction $f$ (rasoir d’Occam) par une fonction linéaire, on a alors \(\text{Attn}(\text{query}, doc_k) = \text{rel}(\text{doc}_k) + b_k + \epsilon\) Donc en gros ils supposent que le score d’attention entre le document et la query est une combinaison linéaire du biais de position et de la pertinence réelle du document avec la query. Pour isoler $\text{rel}(\text{doc}_k)$, ils introduisent un document “dummy” à la même position $k$ que le document: \(\text{doc}_{\text{k;dum}}$, on a alors $\text{rel}(\text{doc}_k) = \text{Attn}(\text{query}, doc_k) - \text{Attn}(\text{query}, doc_{k;dum}) + \epsilon\) Grâce à la pertinence “effective” de chaque document, ils calculent, $\forall k$, un coefficient de rééchelonnement $\alpha_k$, qui est une fonction Softmax appliquée sur le score de pertinence du document $\text{doc}_k$.

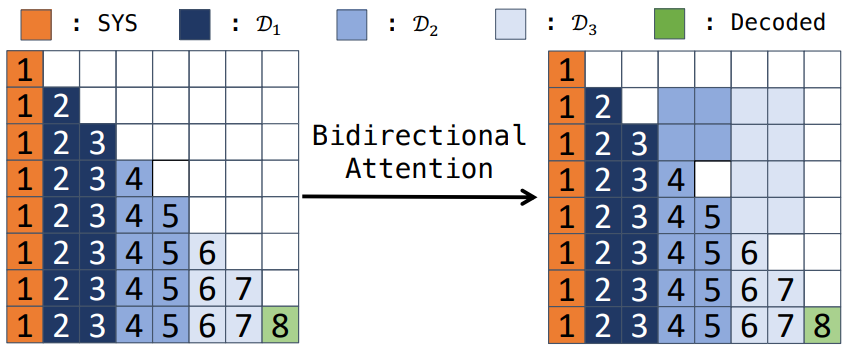
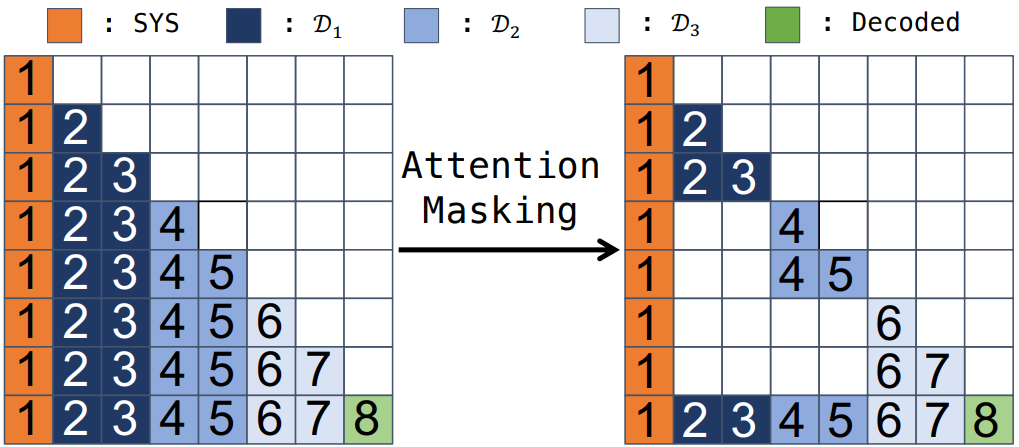
• Attention bidirectionnelle entre documents (PCW 2212.10947) propose une modification de l’attention entre documents pour un traitement “indépendant”: Au lieu d’utiliser l’attention causale (unidirectionnelle) qui impose un ordre strict. A contrario, le papier l’approche d’attention bidirectionnelle entre documents propose une approche d’attention bidirectionnelle qui permet à chaque document d’interagir équitablement avec tous les autres.

</div>
<div class="col-md-6">

</div>

</div>

• Diminuer le biais positionnel dû à RoPE: L’objectif principal de ROPE est d’encoder l’information positionnelle de sorte que le produit scalaire des embeddings de requête et de clé contienne intrinsèquement l’information relative à la position, c’est-à-dire $f(q_m, m)^T f(k_n, n) = f(q_m, k_n, m - n)$. Ici, $f$ est la fonction d’encodage positionnel appliquée aux embeddings de requête et de clé aux positions $m$ et $n$, respectivement. Pour satisfaire cette condition, la fonction $f$ est définie comme une fonction complexe vectorielle :

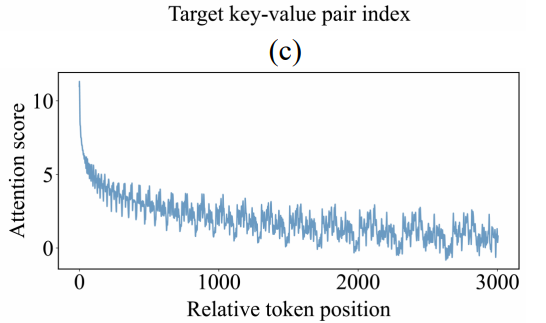
  \[f(x, m) = x e^{im\theta} = \left[(x_1 + i x_2)e^{im\theta_1};(x_3 + i x_4)e^{im\theta_2};\ldots;(x_{l-1} + i x_l)e^{im\theta_{l/2}}\right]^T\]

  Dans cette équation, $l$ représente la dimension des embeddings, $\theta_k = 10000^{-2k/l}$, et $i$ est l’unité imaginaire. Pour le calcul du score d’attention, RoPE considère la partie réelle du produit, spécifiquement $\operatorname{Re}\left(f(q_m, m)^T f(k_n, n)\right)$. La fonction trigonométrique $\cos((m-n) \theta)$ est périodique, d’où la waveform qu’on obtient. pour certaines valeurs de $(m−n)$, le cosinus (et le sinus) prend des valeurs élevées (les “pics”), tandis que pour d’autres il prend des valeurs faibles (les “creux”). Ainsi, si une information cruciale se trouve à une position qui correspond à un trough de l’oscillation, son score d’attention sera relativement bas. La fréquence des oscillations est modulée par rapport à $\theta_k$: Donc ce qui se fait couramment pour contrebalancer ça, c’est de prendre plusieurs bases de $\theta$, qui fixe l’échelle exponentielle à laquelle les fréquences décroissent.

Ainsi, plusieurs approches visent à contre-balancer le biais positionnel induit par RoPE:

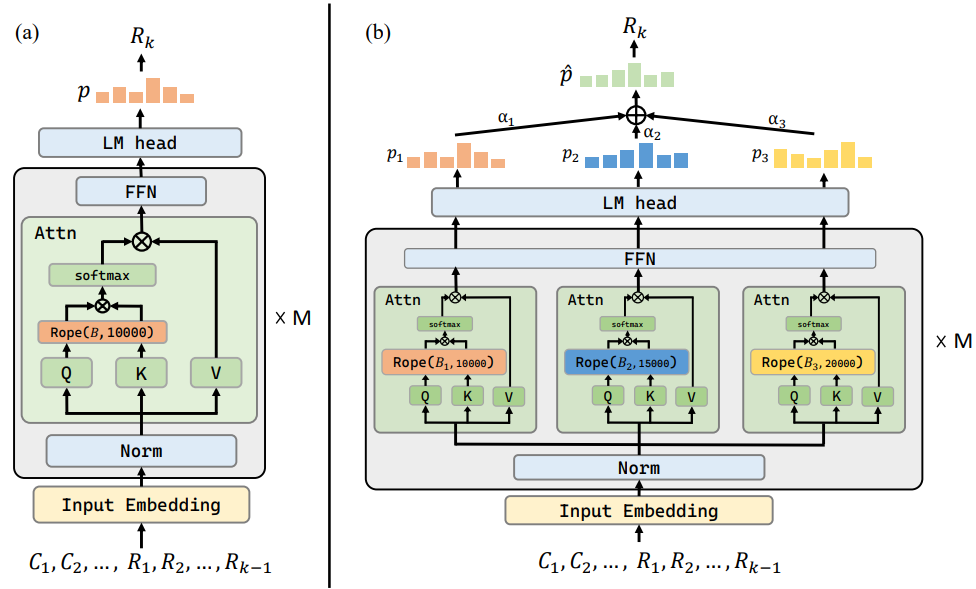
• Attention Bucket (2312.04455)
  Plusieurs bases $\theta$ traitées en parallèle.

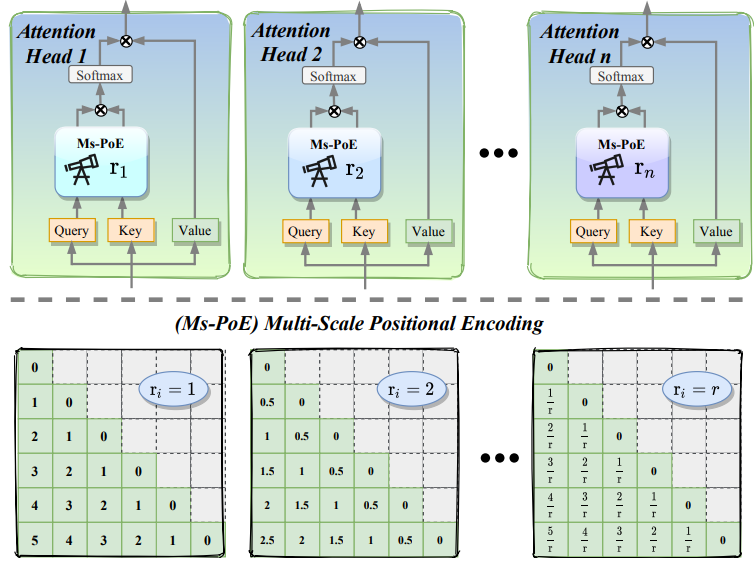
• MS-PoE (2403.04797)
  C’est une approche qui applique un facteur $r$ à la position des tokens par tête, modifiant du coup l’oscillation par tête $m/r \theta$ afin de garder la base RoPE sur laquelle a été entraîné le modèle (dans une approche de correction du biais à l’inférence)

</div>

2. Jouer sur les données

• IN2 training (2404.16811)
  Fine-tuning sur des QA avec contextes longs formés par concaténation aléatoire de segments courts.

• Réordonnancement des documents (ACL-Long’24)
  Placer les plus pertinents en début ou fin de prompt.

Introduction du papier « Mitigate Positional Biais via Scaling a Single Dimension »

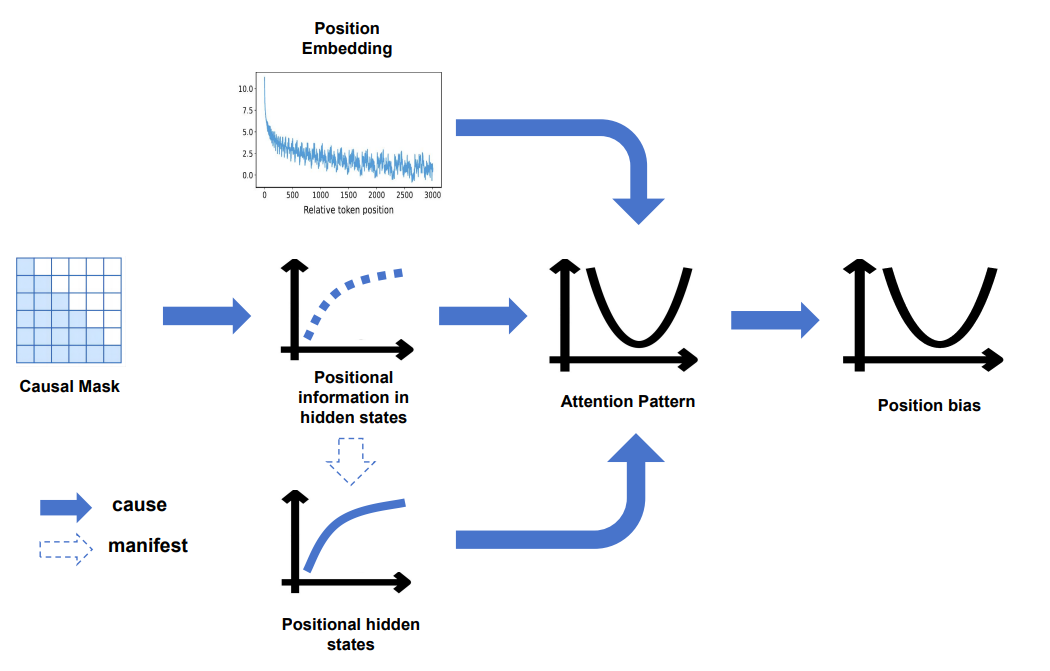
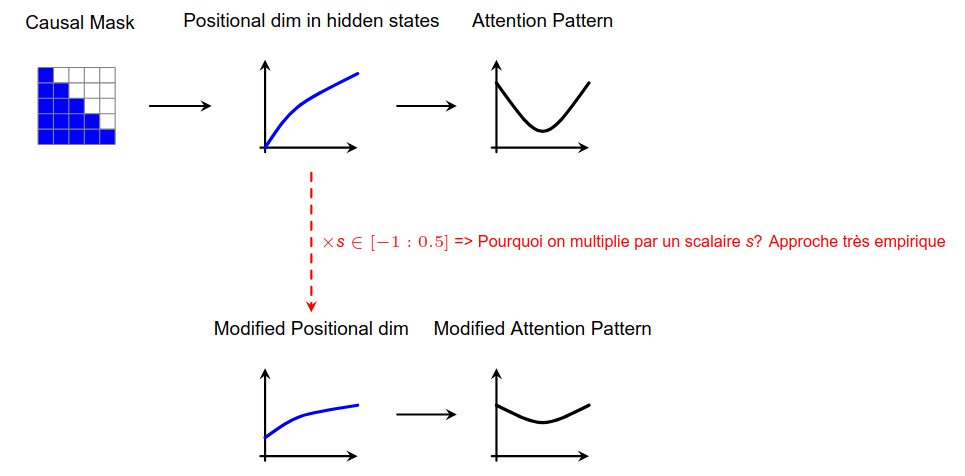
• Le biais positionnel provient des patterns d’attention (focus sur début/fin).
• Causal mask + encodage positionnel génèrent des “dimensions positionnelles” dans les hidden-states.
• Objectifs :
  1. Identifier ces dimensions.
  2. Les modifier (scaling) pour diminuer le biais.

Tâche de retrieval utilisée

• Clés/valeurs aléatoires pour isoler le pure retrieval.

• On mesure

  \[A_G = \frac{1}{|G|} \sum_{j\in G} a_{l,j}\]

  où $l$=dernier token (interrogateur), $G$=positions de la clé, $a_{l,j}$=poids d’attention.

Identification des dimensions positionnelles

1. Monotonie : $h(p)$ doit être strictement croissante ou décroissante.
2. Smoothness : dérivée seconde faible (évolution “douce”).

3. Choix de la dimension $t$ et de l’échelle $s<1$ minimisant la perte

   \[\arg\min_{h_t,s<1} \mathbb{E}\left[\sum_{i=1}^{|P|} \mathcal{L}(x,y,p_i; F(\theta,h_t,s))\right]\]

   avec $F(\theta,h_t,s)$ le modèle scaled sur la $t$-ième dimension.

Construction de $h(p_i)$

• Approximation par moindres carrés segmentés pour lisser le signal.
• Hypothèse : $\textbf{hidden_state}_i = h(p_i) + \epsilon_i$.
• Permet de distinguer tendance monotone et bruit.

Résultats de l’identification

• Tendance monotone dès la couche 1, s’amplifie dans les couches supérieures.

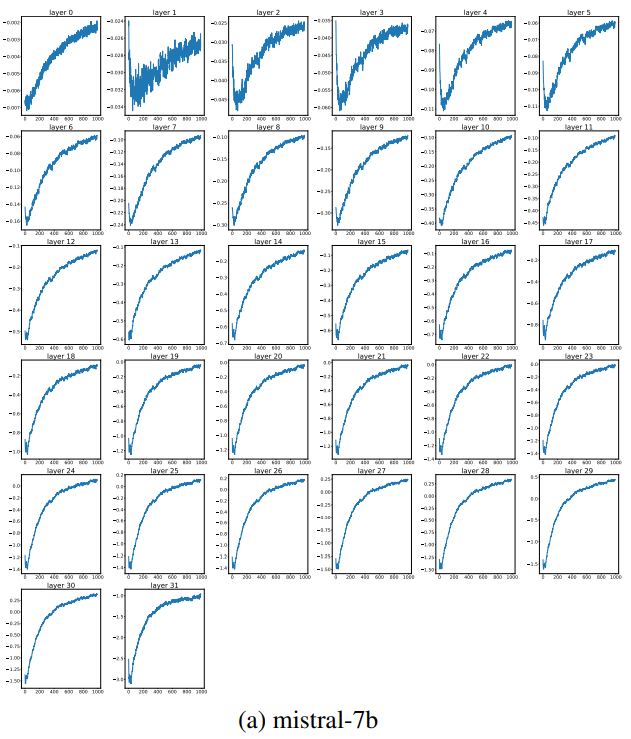
Dimensions causées par le masque causal

• Réduction du PE de 200 pour positions 400–600 : effet mineur.
• Rogner le masque causal pour ces positions : fortes fluctuations.

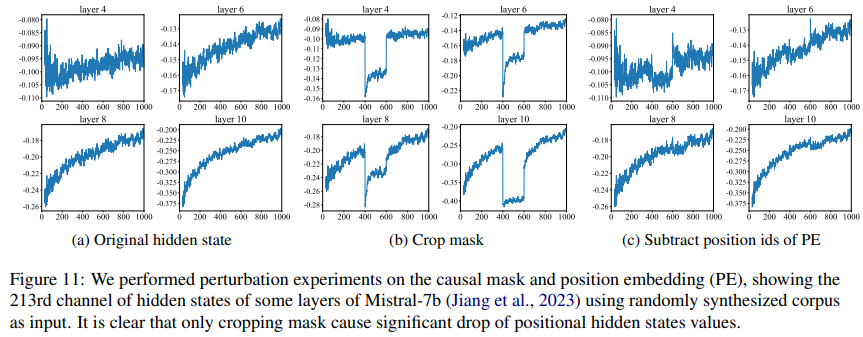
Correction proposée

• Prouvé que la performance biasée vient des patterns d’attention : en doublant le score à la position 25, on déplace l’attention.

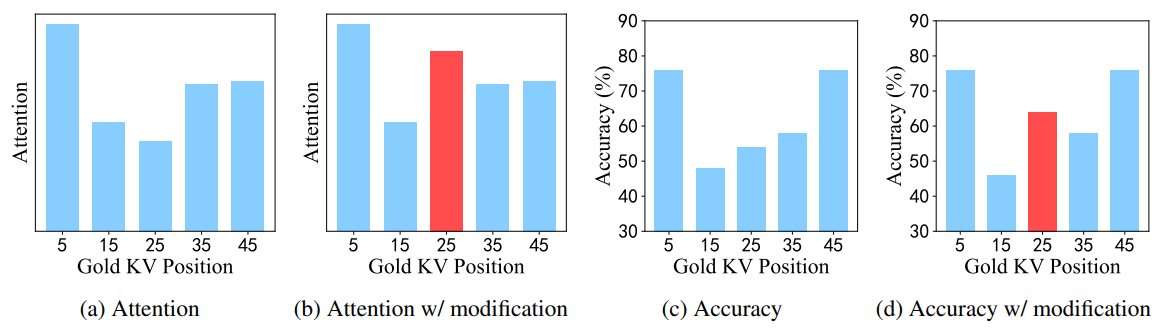
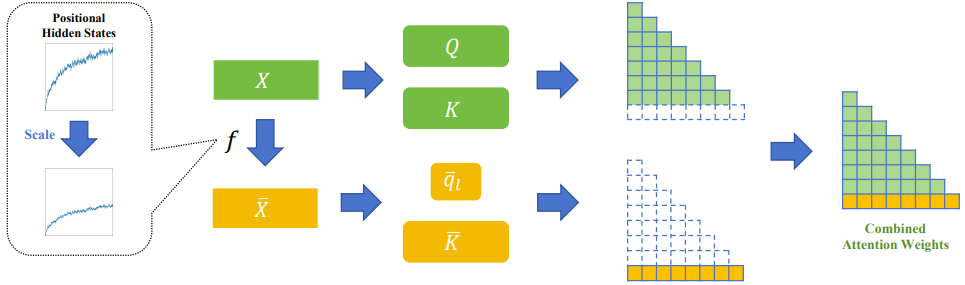
• Modification : scaler la dimension $p$ uniquement pour le calcul du score d’attention du dernier token $l$ :

  \[z = \begin{cases} \mathrm{Softmax}\left((q_i K^\top + \mathrm{Mask})/\sqrt d\right)V, & i<l,\\ \mathrm{Softmax}\left((\bar q_l\;\bar K^\top)/\sqrt d\right)V, & i=l. \end{cases}\]

Effet du scaling

• $s>1$ → focus début ; $s<0$ → focus fin.
• $s\in[-1,0.5]$ → distribution équilibrée.

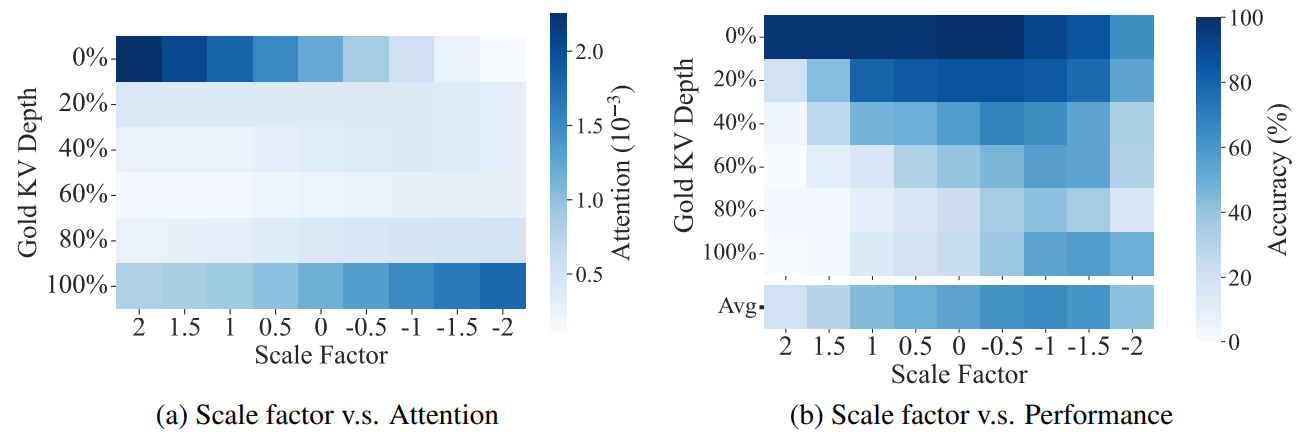
• Varie selon les modèles :

Performances

Gain significatif sur LongBench :

Limitations (selon moi)

1. Hypothèses de monotonie et smoothness de $h(p)$ très discutables et infondées.
2. Lien causal masque => hidden-states pas rigoureusement démontré. le fait qu’il y ait du biais positionnel dans les états cachés est un postulat de départ de ce papier non prouvé proprement.
3. Approche de scaling de “la dimension positionnelle” discutable

Points forts du papier

• Séparation mécanique sémantique vs. position. Un autre papier étudie cette séparation pour comprendre quelle tête ont les parties positionnelles et sémantiques dans les transformers (notamment l’aspect low-rank et low-frequency de la partie positionnelle): Uncovering hidden geometry in Transformers via disentangling position and context. Un autre papier (Exploring Context Window of Large Language Models via Decomposed Positional Vectors) cherche à décomposer les états cachés de chaque token en partie sémantique et positionnelle en faisant une estimation empirique des vecteurs positionnels sur un grand nombre d’exemples.
• Peu de papiers visent à corriger le biais positionnel dû au masque causal, donc j’ai trouvé ce papier intéressant qui s’attaque à cela au lieu de s’attaquer au biais positionnel dû à l’encodage positionnel.

Pour aller plus loin : découpler sémantique et position

Spline-based Transformers (ECCV’25)

• Suppression de l’encodage positionnel.

• Introduction de tokens de contrôle formant une spline :

  \[s(t)=\sum_{i=0}^n N_{i,k}(t)\,\mathbf p_i\]
• Position implicite via la géométrie.

Decomposed Positional Vectors (NeurIPS)

• Décomposition : $h_{l,t}=p_{l,t}+cs_{l,t}$.
• Estimation : $p_{l,t}=\frac{1}{N}\sum_{s=1}^N h^{(s)}_{l,t}$.
• Isolation : $cs_{l,t}=h_{l,t}-p_{l,t}$.