Approches d'explicabilité via attribution de la prédiction aux données d'entrée

Approches d'explicabilité via attribution de la prédiction aux données d'entrée

Explicabilité par localisation des points d’entrée qui ont amené à la prédiction

Les méthodes d’attribution produisent des explications locales pour une entrée spécifique. Elles peuvent attribuer la prédiction locale du modèle à différents types de données :

Approches d’attribution basées sur les gradients

Les méthodes d’attribution basées sur les gradients exploitent les dérivées partielles du modèle par rapport à l’entrée pour quantifier l’importance de chaque élément individuel des données d’entrée pour une prédiction donnée.

L’idée fondamentale est de calculer le gradient de la fonction de sortie par rapport aux différentes coordonnées de l’entrée.

Cartes de saliency obtenues avec différentes approches d'attribution basées sur les gradients pour la prédiction de la classe "Landing Navaids" sur un modèle entraîné sur le dataset de classification NOTAM.

1. Saliency (Gradient simple)

La méthode Saliency calcule le gradient absolu de la sortie du modèle par rapport à son entrée :

\[\boxed{\forall \text{ dimension } i \text{ de } x: \quad S_i = \left|\frac{\partial f(x)}{\partial x_i}\right|}\]

Référence : Simonyan et al. (2013). Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps.

Code Interpreto :

from interpreto import Saliency, Granularity

# Initialiser la méthode Saliency
method = Saliency(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    granularity=Granularity.WORD,  # ALL_TOKENS, TOKEN, WORD, SENTENCE
    input_x_gradient=True,  # Multiplier par l'entrée (Gradient x Input)
)

# Expliquer une prédiction
explanations = method.explain(text)

Limites :

2. Gradient $\times$ Input

Cette méthode multiplie le gradient par la valeur de l’entrée :

\[\boxed{\forall \text{ dimension } i \text{ de } x: \quad S_i = x_i \cdot \frac{\partial f(x)}{\partial x_i}}\]

Le gradient pur $\partial f/\partial x_i$ mesure la sensibilité mais pas la présence ; multiplier par $x_i$ donne un terme sensibilité $\times$ magnitude.

Dans Interpreto, ceci est contrôlé par le paramètre input_x_gradient=True :

# Gradient x Input est activé par défaut
method = Saliency(model, tokenizer, input_x_gradient=True)

3. Integrated Gradients (IG)

Integrated Gradients attribue à chaque feature $i$ une contribution cumulative le long d’un chemin depuis une baseline $x’$ jusqu’à l’entrée $x$.

Avec le chemin linéaire $\gamma(\alpha) = x’ + \alpha(x - x’)$, $\alpha \in [0,1]$, l’attribution est :

\[\boxed{\mathrm{IG}_i(x; x') = (x_i - x'_i) \int_0^1 \frac{\partial f(\gamma(\alpha))}{\partial x_i} \, d\alpha}\]

Référence : Sundararajan et al. (2017). Axiomatic Attribution for Deep Networks.

IG atténue le problème de localité en agrégeant l’information du gradient le long du chemin $\gamma(\alpha)$ de $x’$ à $x$. Même si $\nabla f(x) \approx 0$, il peut y avoir des $\alpha \in (0,1)$ où $\nabla f(\gamma(\alpha))$ est grand.

En NLP, IG est appliqué dans l’espace des embeddings : si $e(x) \in \mathbb{R}^d$ est l’entrée réelle du réseau (embeddings de tokens concaténés), on interpole $e’ + \alpha(e - e’)$ et on différencie $f$ par rapport aux composantes de l’embedding. La baseline $e’$ est souvent le vecteur zéro, un token [PAD], ou un embedding neutre.

Code Interpreto :

from interpreto import IntegratedGradients

method = IntegratedGradients(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    n_perturbations=50,    # Nombre d'interpolations (approximation de Riemann)
    baseline=None,         # None = vecteur zéro, ou torch.Tensor personnalisé
    input_x_gradient=True,
)

explanations = method.explain(text)

4. SmoothGrad

SmoothGrad moyenne les gradients sous des perturbations gaussiennes :

\[\boxed{\delta \sim \mathcal{N}(0, \sigma^2 I), \quad \phi_{\mathrm{SG}}(x) = \mathbb{E}_\delta[\nabla_x f(x + \delta)] \approx \frac{1}{N} \sum_{i=1}^{N} \nabla_x f(x + \delta_i)}\]

avec $\delta_i \stackrel{\text{i.i.d.}}{\sim} \mathcal{N}(0, \sigma^2 I)$.

Référence : Smilkov et al. (2017). SmoothGrad: removing noise by adding noise.

Code Interpreto :

from interpreto import SmoothGrad

method = SmoothGrad(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    n_perturbations=50,   # Nombre d'échantillons
    noise_std=0.1,        # Écart-type du bruit gaussien
    input_x_gradient=True,
)

explanations = method.explain(text)

5. VarGrad

VarGrad calcule la variance des gradients sous perturbations gaussiennes, révélant les régions où le signal de gradient est volatile (explications moins fiables ou fragiles) :

\[\boxed{\phi_{\mathrm{VG}}(x) = \mathrm{Var}_\delta[\nabla_x f(x + \delta)] = \mathbb{E}_\delta\left[(\nabla_x f(x + \delta) - \mu)^2\right]}\]

avec $\mu = \mathbb{E}_\delta[\nabla_x f(x + \delta)]$ (la moyenne calculée par SmoothGrad).

Référence : Adebayo et al. (2018) ; Richter et al. (2020). VarGrad: A Low-Variance Gradient Estimator.

Code Interpreto :

from interpreto import VarGrad

method = VarGrad(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    n_perturbations=50,
    noise_std=0.1,
    input_x_gradient=True,
)

explanations = method.explain(text)

6. SquareGrad

SquareGrad calcule la moyenne des carrés des gradients sous perturbations gaussiennes. Contrairement à SmoothGrad (moyenne) ou VarGrad (variance), SquareGrad capture la magnitude globale de sensibilité indépendamment du signe :

\[\boxed{\phi_{\mathrm{SqG}}(x) = \mathbb{E}_\delta\left[(\nabla_x f(x + \delta))^2\right] \approx \frac{1}{N} \sum_{i=1}^{N} (\nabla_x f(x + \delta_i))^2}\]

Note : $\mathbb{E}[X^2] = \mathrm{Var}(X) + (\mathbb{E}[X])^2$, donc SquareGrad combine les effets de SmoothGrad et VarGrad.

Référence : Hooker et al. (2019). A Benchmark for Interpretability Methods in Deep Neural Networks.

Code Interpreto :

from interpreto import SquareGrad

method = SquareGrad(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    n_perturbations=50,
    noise_std=0.1,
    input_x_gradient=True,
)

explanations = method.explain(text)

7. GradientSHAP

GradientSHAP est un estimateur de valeurs de Shapley basé sur les gradients. Il combine les idées d’Integrated Gradients et de Shapley values en moyennant plusieurs gradients intégrés stochastiques le long de chemins échantillonnés aléatoirement.

Pour une baseline $x’$ échantillonnée et un bruit $\epsilon$ :

\[\boxed{\phi_{\mathrm{GS}}_i(x) = \mathbb{E}_{x' \sim D, \alpha \sim U[0,1]}\left[(x_i - x'_i) \cdot \frac{\partial f(x' + \alpha(x - x') + \epsilon)}{\partial x_i}\right]}\]

où $\epsilon \sim \mathcal{N}(0, \sigma^2 I)$ ajoute du bruit pour améliorer la robustesse.

Référence : Lundberg and Lee (2017). A Unified Approach to Interpreting Model Predictions.

Code Interpreto :

from interpreto import GradientShap

method = GradientShap(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    n_perturbations=20,
    baseline=0,           # Baseline (0 = vecteur zéro)
    noise_std=0.1,        # Bruit ajouté
    input_x_gradient=True,
)

explanations = method.explain(text)

8. GradCAM (CNNs uniquement)

GradCAM utilise à la fois les gradients et les feature maps de la dernière couche convolutionnelle. Elle met en évidence, pour une classe cible $c$, les régions du dernier bloc convolutionnel qui augmentent le score de classe $f_c(x)$.

\[\boxed{\phi = \mathrm{ReLU}\left(\sum_k w_k A^k\right), \quad w_k = \frac{1}{Z} \sum_{i=1}^{W} \sum_{j=1}^{H} \frac{\partial f_c(x)}{\partial A^k_{ij}}}\]

où :

Note : GradCAM n’est applicable qu’aux CNNs et n’est pas disponible directement dans Interpreto (orienté NLP).

Approches d’attribution basées sur les perturbations

Les méthodes par masquage/perturbation construisent une carte d’attribution en substituant des parties de l’entrée et en observant comment le score du modèle change, révélant ainsi les régions sur lesquelles le modèle s’appuie pour sa décision.

1. Occlusion

L’Occlusion utilise un patch de masquage qui glisse sur l’entrée ; à chaque position, la région couverte est remplacée par une constante (ex: 0). L’agrégation des chutes de score sur tous les patches donne la carte de saliency.

Avec $S_c$ la sortie de la couche avant softmax, $\bar{x}$ une baseline :

\[\boxed{\phi_i = S_c(x) - S_c(x_{[x_i = \bar{x}]})}\]

Référence : Zeiler and Fergus (2014). Visualizing and understanding convolutional networks.

Code Interpreto :

from interpreto import Occlusion, Granularity
from interpreto.attributions import InferenceModes

method = Occlusion(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    granularity=Granularity.WORD,
    inference_mode=InferenceModes.SOFTMAX,  # LOGITS, SOFTMAX, LOG_SOFTMAX
)

explanations = method.explain(text)

Limites : L’approche par occlusion cache une région d’une seule manière fixe et mesure la chute de score ; elle est donc sensible à la baseline choisie $\bar{x}$ et à la taille du patch, et ignore les interactions multi-contextes.

2. RISE

RISE (Randomized Input Sampling for Explanation) consiste à échantillonner aléatoirement des masques qui préservent ou suppriment des régions (estimation Monte Carlo), puis à moyenner ces masques pondérés par le score du modèle :

\[\boxed{\phi_i = \mathbb{E}[f(x \odot m) \mid m_i = 1] \approx \frac{1}{\mathbb{E}(\mathcal{M}) \cdot N} \sum_{j=1}^{N} f(x \odot m_j) \cdot m_j}\]

3. LIME

LIME (Local Interpretable Model-agnostic Explanations) explique les prédictions individuelles en ajustant un modèle substitut simple et interprétable localement autour de la prédiction d’intérêt.

Référence : Ribeiro et al. (2016). “Why Should I Trust You?”: Explaining the Predictions of Any Classifier.

Code Interpreto :

from interpreto import Lime, Granularity
from interpreto.attributions import InferenceModes

method = Lime(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    granularity=Granularity.WORD,
    inference_mode=InferenceModes.LOG_SOFTMAX,
    n_perturbations=100,
    perturb_probability=0.5,
    distance_function=Lime.distance_functions.COSINE,  # HAMMING, COSINE, EUCLIDEAN
)

explanations = method.explain(text)

4. Kernel SHAP

KernelSHAP est un estimateur de valeurs de Shapley agnostique au modèle qui interprète les prédictions en calculant les valeurs de Shapley via une régression linéaire pondérée dans l’espace des coalitions de features.

Référence : Lundberg and Lee (2017). A Unified Approach to Interpreting Model Predictions.

Code Interpreto :

from interpreto import KernelShap, Granularity

method = KernelShap(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    granularity=Granularity.WORD,
    n_perturbations=1000,  # Plus de perturbations = meilleure estimation
)

explanations = method.explain(text)

5. Sobol (Analyse de sensibilité)

Sobol est une méthode d’analyse de sensibilité basée sur la variance. Elle quantifie la contribution de chaque composante d’entrée à la variance de la sortie du modèle via échantillonnage Monte Carlo.

Les indices de Sobol mesurent deux types d’effets :

\[\boxed{S_i = \frac{\mathrm{Var}_{X_i}(\mathbb{E}_{X_{\sim i}}[f(X) \mid X_i])}{\mathrm{Var}(f(X))}, \quad S_{Ti} = \frac{\mathbb{E}_{X_{\sim i}}[\mathrm{Var}_{X_i}(f(X) \mid X_{\sim i})]}{\mathrm{Var}(f(X))}}\]

où $X_{\sim i}$ désigne toutes les variables sauf $X_i$.

En pratique, ces indices sont estimés via des séquences quasi-aléatoires (Sobol, Halton, Latin Hypercube) pour un échantillonnage efficace.

Référence : Fel et al. (2021). Look at the variance! Efficient black-box explanations with Sobol-based sensitivity analysis.

Code Interpreto :

from interpreto import Sobol, Granularity
from interpreto.attributions import InferenceModes

method = Sobol(
    model=model,
    tokenizer=tokenizer,
    batch_size=4,
    granularity=Granularity.WORD,
    inference_mode=InferenceModes.LOGITS,
    n_token_perturbations=32,
    sobol_indices_order=Sobol.sobol_indices_orders.FIRST_ORDER,  # ou TOTAL_ORDER
    sampler=Sobol.samplers.SOBOL,  # SOBOL, HALTON, ou LATIN_HYPERCUBE
)

explanations = method.explain(text)

Avantages :

Tableau récapitulatif des méthodes

Méthode Type Classe Interpreto Paramètres clés
Saliency Gradient Saliency input_x_gradient
Gradient × Input Gradient Saliency input_x_gradient=True
Integrated Gradients Gradient IntegratedGradients n_perturbations, baseline
SmoothGrad Gradient SmoothGrad n_perturbations, noise_std
VarGrad Gradient VarGrad n_perturbations, noise_std
SquareGrad Gradient SquareGrad n_perturbations, noise_std
GradientSHAP Gradient GradientShap n_perturbations, baseline, noise_std
Occlusion Perturbation Occlusion granularity
LIME Perturbation Lime n_perturbations, distance_function
Kernel SHAP Perturbation KernelShap n_perturbations
Sobol Perturbation Sobol n_token_perturbations, sobol_indices_order

Limites pour les modèles de langue (NLP)

Les approches d’attribution basées sur les gradients présentent des défis spécifiques pour les modèles de langue :

Problème de la dimension des embeddings

Pour les images, un pixel n’a que quelques canaux (R, G, B), il est donc relativement facile d’agréger en un seul score de saliency par pixel.

En revanche, dans les modèles de langue, l’unité est un token, plus précisément son embedding, qui est de haute dimension ($D = \text{dim_model}$, typiquement 768 pour BERT, 4096+ pour les LLMs).

Agréger les $D$ composantes en un seul score par token n’est pas trivial.

Stratégies d’agrégation dans Interpreto

Dans Interpreto, l’agrégation est effectuée dans inference_wrapper.py :

def _get_gradients_from_mapping(self, model_inputs, targets, input_x_gradient=False):
    # Obtenir les embeddings
    inputs_embeds = model_inputs["inputs_embeds"].detach().requires_grad_(True)  # (n, l, d)

    # Calculer les logits ciblés
    logits = self.get_targeted_logits(model_inputs, targets)  # (n, t)

    list_of_target_wise_grads = []
    for k in range(t):
        # Calculer le gradient pour le k-ième logit ciblé
        target_wise_grads = torch.autograd.grad(
            outputs=logits,
            inputs=inputs_embeds,
            grad_outputs=grad_outputs,
        )[0]  # (n, l, d)

        # Appliquer le truc input_x_gradient si requis
        if input_x_gradient:
            target_wise_grads = target_wise_grads * inputs_embeds

        # AGRÉGATION : moyenne des valeurs absolues sur la dimension cachée 'd'
        aggregated_target_wise_grads = target_wise_grads.abs().mean(dim=-1)  # (n, l)

        list_of_target_wise_grads.append(aggregated_target_wise_grads)

    return torch.stack(list_of_target_wise_grads, dim=1)  # (n, t, l)

Le choix commun est la norme L2 ou la moyenne des valeurs absolues des gradients par dimension, mais cela est discutable :

Stratégies d’agrégation par granularité

Interpreto propose aussi des stratégies pour agréger les scores de tokens en scores de mots/phrases via GranularityAggregationStrategy :

from interpreto import Granularity
from interpreto.commons.granularity import GranularityAggregationStrategy

method = Saliency(
    model=model,
    tokenizer=tokenizer,
    granularity=Granularity.WORD,  # Agréger au niveau mot
    granularity_aggregation_strategy=GranularityAggregationStrategy.MEAN,  # MEAN, MAX, MIN, SUM, SIGNED_MAX
)

Les options disponibles :

Explicabilité par les concepts: du “où” au “quoi”

Les méthodes d’attribution d’entrée (input attribution) révèlent “où” le modèle regarde dans les données d’entrée pour faire sa prédiction, mais échouent à expliquer “ce que” le modèle voit dans ces zones.

Les approches d’attribution basées sur les concepts consistent à trouver des concepts interprétables par l’humain dans l’espace d’activation d’un réseau de neurones.

Ces approches tentent de répondre à la question : Que voit le modèle dans les zones qu’il regarde pour sa prédiction ?

Le principe général est de :

  1. Analyser les concepts à partir d’une entrée avec des approches non supervisées
  2. Attribuer un score d’importance à ces zones de l’entrée contenant ces concepts vis-à-vis de la prédiction du modèle (en utilisant des approches de saliency vues précédemment)

ACE : Automatic Concept-based Explanations

Le premier travail dans ce domaine, utilisant des approches non supervisées pour détecter les concepts, est ACE (Ghorbani et al., 2019). Cette méthode repose sur une combinaison de segmentation et de techniques de clustering pour identifier les concepts.

Fonctionnement d’ACE

  1. Segmentation : Chaque image est segmentée en régions
  2. Extraction des activations : Les activations intermédiaires du réseau sont extraites pour chaque segment, qui est redimensionné à la taille d’entrée appropriée et rempli avec une valeur de référence
  3. Clustering : Ces activations sont ensuite regroupées en clusters
  4. Post-traitement : Certains concepts contiennent des segments de “fond” (background), donc une étape de post-traitement supprime ces concepts inutiles

Limitation principale

Chaque segment d’image ne peut appartenir qu’à un seul cluster, ce qui n’est pas compatible avec l’idée de superposition de features (phénomène de “superposition” des caractéristiques dans les réseaux de neurones).

CRAFT : Concept Recursive Activation FacTorization

La bibliothèque CRAFT de Deel-ai utilise une autre approche non supervisée pour la découverte de concepts : la Factorisation en Matrices Non-Négatives (NMF) dans les espaces latents.

Cette approche considère la superposition de features : ici, un concept = une direction latente positive des activations $A$.

Formulation mathématique

\[(\mathbf{U}, \mathbf{W}) = \arg \min_{\mathbf{U} \geq 0, \, \mathbf{W} \geq 0} \frac{1}{2} \left\| \mathbf{A} - \mathbf{U}\mathbf{W}^\top \right\|_F^2\]

où :

Le coefficient $U(i,j)$ quantifie la contribution (ou présence) du concept $j$ dans la reconstruction du vecteur d’activation de l’image $i$ sous un modèle additif non-négatif.

Pipeline CRAFT

  1. Sélectionner un ensemble d’images du dataset étiquetées avec la même classe
  2. Sélectionner une fonction de découpage $\pi(\cdot)$ pour créer des sous-régions $X_i$ de l’image $X$
  3. Obtenir les activations $A_i = g(X_i)$ des crops aléatoires
  4. Appliquer la NMF pour décomposer les activations positives $A$ en un produit de matrices non-négatives de rang faible $U$ et $W$
  5. Une fois la banque de concepts $W$ pré-calculée, on peut associer les coefficients de concept $u$ à toute nouvelle entrée $x$ en résolvant le problème NNLS (Non-Negative Least Squares) :
\[\min_{u \geq 0} \; \frac{1}{2} \left\| g(x) - u \mathbf{W}^\top \right\|_F^2\]

Code CRAFT (PyTorch)

Voici l’implémentation principale de la méthode fit dans CRAFT :

from sklearn.decomposition import NMF

class Craft(BaseConceptExtractor):
    def __init__(self, input_to_latent: Callable,
                       latent_to_logit: Optional[Callable] = None,
                       number_of_concepts: int = 20,
                       batch_size: int = 64,
                       patch_size: int = 64,
                       device: str = 'cuda'):
        super().__init__(input_to_latent, latent_to_logit, number_of_concepts, batch_size)
        self.patch_size = patch_size
        self.device = device

    def fit(self, inputs: np.ndarray):
        """
        Fit the Craft model to the input data.

        Parameters
        ----------
        inputs : np.ndarray
            Input data of shape (n_samples, channels, height, width).

        Returns
        -------
        (patches, U, W) : tuple
            crops, concepts values, and concepts basis.
        """
        image_size = inputs.shape[2]
        strides = int(self.patch_size * 0.80)

        # Extraction des patches
        patches = torch.nn.functional.unfold(inputs, kernel_size=self.patch_size, stride=strides)
        patches = patches.transpose(1, 2).contiguous().view(-1, 3, self.patch_size, self.patch_size)

        # Obtention des activations
        activations = _batch_inference(self.input_to_latent, patches, self.batch_size,
                                       image_size, device=self.device)

        # Global Average Pooling si activations 4D
        if len(activations.shape) == 4:
            activations = torch.mean(activations, dim=(2, 3))

        # Application de la NMF
        reducer = NMF(n_components=self.number_of_concepts)
        U = reducer.fit_transform(activations.numpy())
        W = reducer.components_.astype(np.float32)

        self.reducer = reducer
        self.W = np.array(W, dtype=np.float32)

        return patches, U, W

La méthode transform permet ensuite de projeter de nouvelles entrées dans l’espace des concepts :

def transform(self, inputs: np.ndarray, activations: Optional[np.ndarray] = None):
    """Transform inputs into concept embeddings."""
    self.check_if_fitted()

    if activations is None:
        activations = _batch_inference(self.input_to_latent, inputs, self.batch_size,
                                       device=self.device)

    is_4d = len(activations.shape) == 4
    if is_4d:
        # (N, C, W, H) -> (N * W * H, C)
        activation_size = activations.shape[-1]
        activations = activations.permute(0, 2, 3, 1)
        activations = torch.reshape(activations, (-1, activations.shape[-1]))

    # Projection dans l'espace des concepts via NMF
    U = self.reducer.transform(activations.numpy().astype(self.W.dtype))

    if is_4d:
        # (N * W * H, R) -> (N, W, H, R)
        U = np.reshape(U, (-1, activation_size, activation_size, U.shape[-1]))

    return U

Quel espace latent considérer ?

Application récursive de la NMF

Plus on avance dans les couches du réseau, plus les activations convergent vers leur moyenne de classe (Papyan, 2020). Par conséquent, les concepts deviennent progressivement plus larges et finissent par fusionner en un “concept de niveau classe” dans les dernières couches.

CRAFT applique donc la NMF de manière récursive à travers les couches : on commence par la dernière couche pour obtenir un concept grossier, puis on remonte d’une couche et on applique la NMF sur le sous-ensemble d’images qui activent fortement ce concept grossier, le décomposant en sous-concepts plus spécifiques.

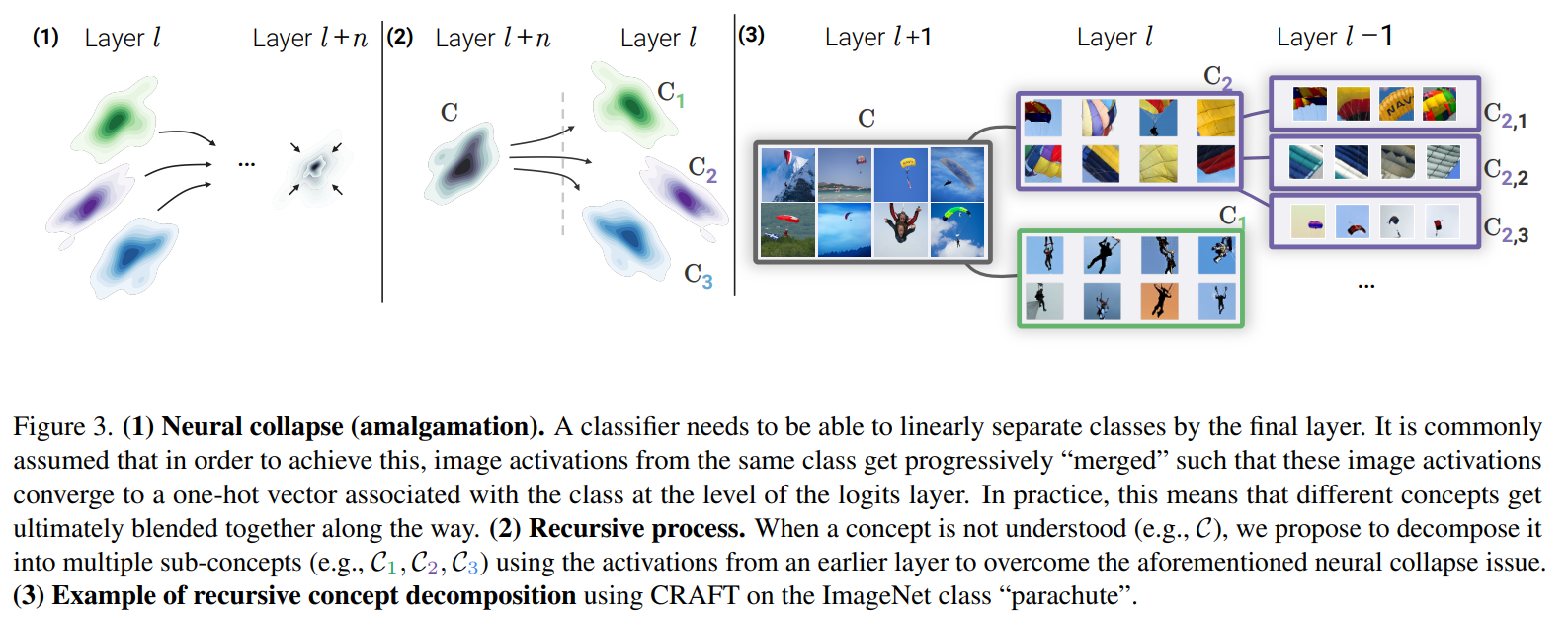
Mais attention, dans la librairie Craft (ou dans Xplique) il n’y a pas l’aspect recursif, cf Craft/issues/4.

Global Average Pooling avant NMF

CRAFT n’applique pas la NMF directement sur les feature maps convolutionnelles. Les dimensions spatiales sont d’abord agrégées (via global average pooling), et la NMF est appliquée aux vecteurs d’activation résultants.

Ce design garantit que les concepts sont définis indépendamment de la position spatiale, la localisation étant gérée uniquement a posteriori via les cartes d’attribution de concepts.

Note : ICE (Zhang et al., 2021) appliquait la factorisation matricielle au niveau des feature maps convolutionnelles, menant à des concepts spatialement conditionnés qui peuvent représenter la même sémantique à différentes positions.

Localisation des concepts dans l’image

CRAFT localise un concept en calculant la sensibilité de son score d’activation par rapport aux feature maps convolutionnelles sous-jacentes.

Pour un concept $j$ donné, CRAFT différencie le coefficient de concept $U(x,j)$ par rapport aux activations spatiales d’une couche convolutionnelle intermédiaire. Ce gradient est ensuite agrégé à travers les canaux à la manière de Grad-CAM pour produire une carte d’attribution de concept.

Importance globale via indices de Sobol

CRAFT utilise ensuite les indices de Sobol pour estimer l’importance globale de chaque concept en mesurant comment les perturbations des coefficients de concept individuels affectent la sortie du modèle.

def estimate_importance(self, inputs, class_id, nb_design=32):
    """
    Estimates the importance of each concept for a given class.
    Uses Sobol total indices as importance scores.
    """
    self.check_if_fitted()
    U = self.transform(inputs)

    masks = HaltonSequence()(self.number_of_concepts, nb_design=nb_design).astype(np.float32)
    estimator = JansenEstimator()

    importances = []
    for u in U:
        u_perturbated = u[None, :] * masks
        a_perturbated = u_perturbated @ self.W

        y_pred = _batch_inference(self.latent_to_logit, a_perturbated, self.batch_size,
                                  device=self.device)
        y_pred = y_pred[:, class_id]

        stis = estimator(masks, y_pred.numpy(), nb_design)
        importances.append(stis)

    return np.mean(importances, 0)

COCKATIEL : Extension au NLP

COCKATIEL étend la philosophie “NMF + ranking + localisation” de CRAFT au texte en remplaçant les crops d’images et les heatmaps spatiales par des extraits textuels et des attributions au niveau des tokens/phrases.

Fonctionnement

  1. Factorisation : Factorisation d’un embedding de haut niveau non-négatif d’extraits textuels via NMF pour découvrir des concepts latents
  2. Ranking : Classement de ces concepts via les indices de sensibilité de Sobol pour évaluer leur importance causale pour les prédictions du modèle
  3. Localisation : Identification des mots ou clauses qui supportent chaque concept dans une instance donnée via un mécanisme d’attribution basé sur l’occlusion

Hypothèses

COCKATIEL suppose uniquement que le modèle entraîné peut être décomposé comme \(f(x) = c(h(x))\) où :

Pour les classifieurs basés sur les transformers (modèles BERT-like), le token spécial [CLS] joue souvent un rôle central, car son état caché final est couramment utilisé comme entrée de la tête de classification.

Interpreto : Boîte à outils pour l’explicabilité NLP

Interpreto est un outil proposant différentes méthodes d’attribution de concepts pour les tâches de classification NLP (ainsi que de génération).

Méthodes de décomposition disponibles

Interpreto utilise plusieurs techniques de décomposition sklearn via son module sklearn_wrappers.py :

1. ICA (Independent Component Analysis)

L’ICA recherche des composantes statistiquement indépendantes :

from sklearn.decomposition import FastICA

class ICAWrapper(SkLearnWrapper):
    def fit(self, x: torch.Tensor, return_sklearn_model: bool = False):
        ica = FastICA(n_components=self.nb_concepts, random_state=self.random_state, max_iter=500)
        ica.fit(x.detach().cpu().numpy())

        self.mean.data = torch.as_tensor(ica.mean_, dtype=torch.float32)
        self.components.data = torch.as_tensor(ica.components_.T, dtype=torch.float32)
        self.mixing.data = torch.as_tensor(ica.mixing_.T, dtype=torch.float32)
        self.fitted = True

    def encode(self, x: torch.Tensor) -> torch.Tensor:
        """Project into concept space: z = (x - mean) @ components"""
        return (x - self.mean) @ self.components

    def decode(self, z: torch.Tensor) -> torch.Tensor:
        """Reconstruct from concepts: x = z @ mixing + mean"""
        return (z @ self.mixing) + self.mean

2. PCA (Principal Component Analysis)

La PCA trouve les directions de variance maximale :

from sklearn.decomposition import PCA

class PCAWrapper(SkLearnWrapper):
    def fit(self, x: torch.Tensor, return_sklearn_model: bool = False):
        pca = PCA(n_components=self.nb_concepts, random_state=self.random_state)
        pca.fit(x.detach().cpu().numpy())

        self.mean.data = torch.as_tensor(pca.mean_, dtype=torch.float32)
        self.components.data = torch.as_tensor(pca.components_, dtype=torch.float32)
        self.fitted = True

    def encode(self, x: torch.Tensor) -> torch.Tensor:
        return (x - self.mean) @ self.components.T

    def decode(self, z: torch.Tensor) -> torch.Tensor:
        return (z @ self.components) + self.mean

3. SVD (Singular Value Decomposition)

La SVD décompose \(A = U \times S \times V^T\) :

from sklearn.decomposition import TruncatedSVD

class SVDWrapper(SkLearnWrapper):
    def fit(self, x: torch.Tensor, return_sklearn_model: bool = False):
        svd = TruncatedSVD(n_components=self.nb_concepts, random_state=self.random_state)
        svd.fit(x.detach().cpu().numpy())
        self.components.data = torch.as_tensor(svd.components_, dtype=torch.float32)
        self.fitted = True

    def encode(self, x: torch.Tensor) -> torch.Tensor:
        return x @ self.components.T

    def decode(self, z: torch.Tensor) -> torch.Tensor:
        return z @ self.components

4. K-Means

K-Means utilise les centres de clusters comme concepts :

from sklearn.cluster import KMeans

class KMeansWrapper(SkLearnWrapper):
    def fit(self, x: torch.Tensor, return_sklearn_model: bool = False):
        kmeans = KMeans(n_clusters=self.nb_concepts, random_state=self.random_state)
        kmeans.fit(x.detach().cpu().numpy())
        self.components.data = torch.as_tensor(kmeans.cluster_centers_, dtype=torch.float32)
        self.fitted = True

    def encode(self, x: torch.Tensor) -> torch.Tensor:
        """Returns distances to cluster centers"""
        return torch.cdist(x, self.components, p=2)

Utilisation avec Interpreto

from interpreto import ModelWithSplitPoints
from interpreto.concepts import ICAConcepts, PCAConcepts, NMFConcepts
from interpreto.concepts.interpretations import TopKInputs

# 1. Diviser le modèle en deux parties
splitted_model = ModelWithSplitPoints(
    model, tokenizer=tokenizer, split_points=[5],
)

# 2. Calculer les activations
activations = splitted_model.get_activations(
    dataset, activation_granularity=WORD
)

# 3. Choisir une méthode de décomposition et fit
explainer = ICAConcepts(splitted_model, nb_concepts=20)
# Ou: explainer = PCAConcepts(splitted_model, nb_concepts=20)
# Ou: explainer = NMFConcepts(splitted_model, nb_concepts=20, force_relu=True)
explainer.fit(activations)

# 4. Interpréter les concepts
interpreter = TopKInputs(
    concept_explainer=explainer,
    activation_granularity=WORD,
)
interpretations = interpreter.interpret(
    inputs=dataset, latent_activations=activations
)

# Afficher les interprétations
for concept_id, words in interpretations.items():
    print(f"Concept {concept_id}: {list(words.keys())}")

Classes d’explainer disponibles dans Interpreto

Méthode Classe Description
NMF NMFConcepts Factorisation non-négative (Lee & Seung, 1999)
Semi-NMF SemiNMFConcepts NMF avec \(W\) pouvant être négatif (Ding et al., 2008)
Convex-NMF ConvexNMFConcepts NMF convexe (Ding et al., 2008)
ICA ICAConcepts Analyse en composantes indépendantes (Hyvarinen & Oja, 2000)
PCA PCAConcepts Analyse en composantes principales (Pearson, 1901)
SVD SVDConcepts Décomposition en valeurs singulières
K-Means KMeansConcepts Clustering K-Means
Sparse PCA SparsePCAConcepts PCA sparse
Dictionary Learning DictionaryLearningConcepts Apprentissage de dictionnaire (Mairal et al., 2009)
Vanilla SAE VanillaSAEConcepts Sparse Autoencoder (Cunningham et al., 2023)
TopK SAE TopKSAEConcepts SAE avec activation TopK (Gao et al., 2024)
JumpReLU SAE JumpReLUSAEConcepts SAE avec JumpReLU (Rajamanoharan et al., 2024)

Comparaison des approches

Aspect ACE CRAFT COCKATIEL
Domaine Vision Vision NLP
Méthode Segmentation + Clustering NMF NMF
Superposition Non Oui Oui
Localisation Segments Grad-CAM-like Occlusion
Importance - Indices de Sobol Indices de Sobol

Here is a notebook testing these methods on a text classification task (on NOTAM dataset):

Sorry, the notebook you are looking for does not exist.

Références