Les fonctions d'influence appliquées aux LLMs

Détail de ma compréhension des fonctions d'influence appliquées aux LLMs

J’ai eu l’opportunité au sein d’Orange d’explorer les fonctions d’influences appliquées au deep learning, un concept introduit notamment dans le papier Understanding Black-box Predictions via Influence Functions. Ces fonctions permettent de quantifier l’impact d’une donnée d’entraînement sur une prédiction du modèle. Elles approximent en réalité la méthode “Leave-one-out” qui compare la prédiction du modèle avec et sans cet échantillon dans le dataset d’entraînement (en entraînant le modèle sans et avec). Cette approche m’a particulièrement intéressée dans le contexte des modèles de langage (LLMs). En travaillant sur l’adaptation d’un LLM à un domaine spécifique, j’ai été confrontée à une question cruciale : comment sélectionner les données de fine-tuning pour garantir que le modèle puisse répondre efficacement à des questions spécifiques? On s’était confronté à plusieurs défis dans le cadre de ce projet sur l’adaptation des LLMs à un domaine métier: Comment identifier quelles données permettent réellement d’améliorer les performances sur des tâches ciblées? Comment évaluer l’impact du “continual pretraining” de mon LLM sur un texte précis sur la performance du modèle final sur la tâche cible? Ainsi, j’ai décidé d’étudier un peu plus en détail les fonctions d’influence appliquées aux LLMs et j’ai trouvé ça facinant (et mathématiquement parlant très complexe). Donc je me suis dit que ça serait utile d’en faire un post, et de mettre un peu les différents papiers que j’ai lu (en diagonale ou de manière plus approfondie), ce que j’ai compris des formules, des approximations, des approches pour adaptées ces méthodes aux LLMs, etc. Ce post est un condensé de tout cela!

Introduction à ce post

Comme expliqué précédemment, l’influence cherche à approximer le Leave-one-out, c’est à dire cherche à estimer l’impact qu'aurait un exemple d'entraînement sur la perte d'un exemple de test (ou sur plusieurs résultats du modèle sur un jeu de données test).

Dans l’ensemble de ce post, on va montrer d’où sort la formule suivante, comment elle est adaptée pour son application aux LLMs, et des cas concrets de son application:

\[\begin{split} \mathrm{Influence}\bigl(z_{\mathrm{train}}\to z_{\mathrm{test}}\bigr) &= \frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\,\theta_\varepsilon(z_\text{train})\bigr)\Big|_{\varepsilon=0} \\ &\approx -\nabla_\theta \,\mathcal{L}\bigl(z_{\mathrm{test}},\,\hat{\theta} \bigr)\,H_\theta^{-1}(\hat{\theta})\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \\ &\approx -\nabla_\theta \,\mathcal{L}\bigl(z_{\mathrm{test}},\,\hat{\theta} \bigr)\,(G_\theta(\hat{\theta}) + \lambda I)^{-1}\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \end{split}\]

Où:

• \(\hat{\theta}\) sont les poids du modèle préentraîné (poids supposés optimiaux pour le jeu de pretraining du LLM)
• \(\theta_\varepsilon(z_\text{train})\) sont les poids du modèle “modifié”, ie lorsqu’on upweight de $\varepsilon$ l’exemple d’entraînement $z_\text{train}$
• \(\theta\) est une variable muette (eg pour le gradient, on dérive par rapport aux paramètres du modèle et on applique en un point)
• Tous les $\theta$ sont des vecteurs colonne des poids du modèle
• $\mathcal{L}$ est la loss du modèle, donc ici, vu qu’on est dans le cas des LLMs, c’est la cross-entropy loss (negative log-likelihood), ie pour une séquence de taille $T$ ($x_1$, $x_2$, …, $x_T$): \(\mathcal{L} = -\frac{1}{T}\sum_{t=1}^{T} \log P(x_t \mid x_1, x_2, \ldots, x_{t-1})\)
• $f$ est une fonction (moyenne, ou autre) sur plusieurs résultats du modèle sur un jeu de données test noté $x$. Il nous permet de ne pas évaluer l’impact de l’upweight d’un $z_\text{train}$ sur la loss d’un $z_\text{test}$, mais sur un ensemble de type de données $x$ (car parfois, on ne veut pas calculer l’influence d’une donnée d’entraînement sur la loss d’un prompt, mais sur la performance (pas forcément la loss d’ailleurs) sur un certain type de prompt)
• $H_\theta$ est la hessienne (dérivée seconde par rapport aux paramètres du modèle)
• $G_\theta$ est la Hessienne de Gauss-Newton qu’on va voir plus loin dans ce post, qui est en fait une approximation de la hessienne
• $\lambda$ est un terme dit de “damping”, dû au fait que la loss n’est pas convexe, qu’on verra plus loin dans le post

Note que dans tout ce post, on va utiliser ces notations!

La librairie Kronfluence permet de calculer l’influence dans le cas des LLMs. D’autres livrairies existent, comme Influenciae ou nngeometry. Les fonctions d’influence permettent de répondre à ce genre de questions:

• Est-ce que je devrais ajouter cet exemple dans mon set d'apprentissage pour améliorer les performances de cette prédiction?
• Quels exemples d'entraînement ont été utiles à la prédiction de mon modèle?
• Le modèle s’est trompé: sur quels exemples d’entraînement s’est-il basé pour cette mauvaise prédiction?

1.1 Introduction sur les fonctions d’influence

Pour introduire les fonctions d’influence appliquées au deep learning, nous nous basons sur le le papier Understanding Black-box Predictions via Influence Functions, et notamment sur l’annexe A pour expliquer les différentes formules.

L’influence de $z_{\rm train}$ sur $z_{\rm test}$ ($\mathrm{Influence}(z_{\rm train} \to z_{\rm test})$) se définit comme

\[\mathrm{Influence}(z_{\rm train}\to z_{\rm test})\;=\; \left.\frac{d}{d\varepsilon}\,\mathcal{L}\bigl(z_{\rm test},\,\theta_\varepsilon(z_\text{train})\bigr)\right|_{\varepsilon=0}\]

L’influence de $z_{\rm train}$ sur $f(x)$ ($\mathrm{Influence}(z_{\rm train} \to f_{\theta_\varepsilon(z_\text{train})}(x))$) se définit comme

\[\mathrm{Influence}(z_{\rm train}\to f(x))\;=\; \left.\frac{d}{d\varepsilon}\,(f_{\theta_\varepsilon(z_\text{train})}(x)\bigr)\right|_{\varepsilon=0}\]

En d’autres termes, elle mesure la sensibilité de la loss de $z_{\rm test}$ (ou de toute fonction $f(x)$) à un « up-weight » infinitésimal de la loss de $z_{\rm train}$.

A noter:

• C’est l’impact de l”up-weight” de la loss sur $z_\text{train}$ sur qqch qu’on mesure avec les fonctions d’influence. En fait pour mesurer l’impact de l”up-weight” de $z_{\text{train}}$ dans la loss globale, on se pose la question: “on se pose la question : “si je donnais un peu plus de poids à ce terme de loss dans l’objectif global, comment cela ferait-il bouger mes paramètres et, avec ces nouveaux paramètres, ma performance sur un point de test, ou sur une fonction?“ . En effet, en deep learning, modifier le poids d’une donnée dans l’entraînement, c’est modifier le poids qu’on donne à sa loss dans l’apprentissage.
• $f_{\theta_\varepsilon(z_\text{train})}(x)$ peut être n'importe quelle fonction (exemple: la moyenne des prédictions sur un ensemble de données types $x$ (cf le papier Which Data Attributes Stimulate Math and Code Reasoning? An Investigation via Influence Functions qui cherche à calculer l’influence des textes d’entraînement sur la génération de code (moyenne de des log probabilité de la génération de chaque token de code générés dans un benchmark sachant un problème de code en langage naturel à résoudre)), la différence entre 2 prédictions du modèle, …)

Nous allons, dans ce post, entrer dans le détail de comment on calcule cette influence:

\[\begin{split} \mathrm{Influence}\bigl(z_{\mathrm{train}}\to z_{\mathrm{test}}\bigr) &= I_{z_\text{test}}\bigl(z_{\mathrm{train}}\bigr) \\ &= \frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\ \theta_\varepsilon(z_\text{train})\bigr) \Big|_{\varepsilon=0} \\ &= -\nabla_\theta \,\mathcal{L}\bigl(z_{\mathrm{test}},\,\hat{\theta}\bigr)\,H_\theta^{-1}(\hat{\theta})\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \end{split}\]

Ou bien, si on veut l’influence sur $f(x)$:

\[\begin{split} \mathrm{Influence}\bigl(z_{\mathrm{train}}\to f(x)\bigr) &= I_{f(x)}\bigl(z_{\mathrm{train}}\bigr) \\ &= \left.\frac{d}{d\varepsilon}\bigl(f_{\theta_{\varepsilon}(z_{\mathrm{train}})}(x)\bigr)\right|_{\varepsilon=0} \\ &= - \nabla_\theta f_{\hat{\theta}}(x)^\top \, H_\theta(\hat{\theta})^{-1} \, \nabla_\theta \mathcal{L}\bigl(x_{\mathrm{train}},\hat{\theta}\bigr) \end{split}\]

On cherche donc à calculer

\[\frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\ \theta_\varepsilon(z_\text{train})\bigr) \Big|_{\varepsilon=0}\]

1.1.1. Décomposition avec chain rule

On peut voir \(\frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\ \theta_\varepsilon(z_\text{train})\bigr) \Big|_{\varepsilon=0}\) comme : \(\frac{d}{d\varepsilon} f(g(\varepsilon))\)

avec :

• $g(\varepsilon) = \theta_\varepsilon(z_\text{train})$
• $f(\theta_\varepsilon(z_\text{train})) = \mathcal{L}(z_{\rm test},\theta_\varepsilon(z_\text{train}))$

d’où, par chain rule ( \(\frac{d}{d\varepsilon} f \circ g(\varepsilon) = \nabla_\theta f(g(\varepsilon)) \times \frac{d}{d\varepsilon} g(\varepsilon)\) ), on a :

\[\colorbox{yellow}{ $\displaystyle \frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\ \theta_\varepsilon(z_\text{train})\bigr) \Big|_{\varepsilon=0} = \nabla_\theta \mathcal{L}(z_{\rm test}, \hat{\theta}) \times \frac{d}{d\varepsilon} \theta_\varepsilon(z_\text{train}) \Big|_{\varepsilon=0} $}\]

Du coup, dans un premier temps, il nous faut calculer

\[\colorbox{yellow}{ $\displaystyle \frac{d}{d\varepsilon} \theta_\varepsilon(z_\text{train}) \Big|_{\varepsilon=0} $}\]

1.1.2. Calcul de $\frac{d}{d\varepsilon} \theta_\varepsilon(z_\text{train}) \Big|_{\varepsilon=0}$

Calculer cela revient à se demander : comment $\theta_\varepsilon(z_\text{train})$ varie autour de $\theta$ quand on up-weight très légèrement (voisinage de 0) la loss de notre exemple $z_\text{train}$?

Le but ici est de calculer la dérivée de $\theta_\varepsilon(z_\text{train})$ par rapport à $\varepsilon$ pris en $\varepsilon = 0$.

Essayons d’abord de voir ce qu’est ce $\theta_\varepsilon(z_\text{train})$.

Pour faire cet "up-weight" de la loss de $z_{\text{train}}$ d'un tout petit $\varepsilon$, on perturbe la fonction de perte en ajoutant un petit coefficient $\varepsilon$ sur la perte de $z_{\rm train}$ et on voit comment les paramètres optimaux $\theta$ évoluent avec $\varepsilon$.

On repart de ce que ça veut dire de “perturber la fonction de perte en ajoutant un petit coefficient $\varepsilon$ sur la perte de $z_{\rm train}$”: on obtient une nouvelle la loss totale du modèle ($R_\varepsilon(\theta, z_\text{train})$) avec les nouveau poid $\varepsilon$ donné à la loss de $z_{\text{train}}$:

1.1.2.1. $\theta_\varepsilon(z_\text{train})$ sont les poids qui minimisent cette nouvelle loss du modèle après l’upweight de $\varepsilon$ de $z_\text{train}$

Le modèle réentraîné avec cet “upweight” de $\varepsilon$ de $z_\text{train}$ a donc une nouvelle loss de:

\[R_\varepsilon(\theta, z_\text{train}) = \frac{1}{n}\sum_{i=1}^n \mathcal{L}(z_i,\theta) \;+\;\varepsilon\,\mathcal{L}(z_{\rm train},\theta).\]

Puis, on cherche les poids $\theta_\varepsilon(z_\text{train})$ qui minimisent cette nouvelle loss:

\[\theta_\varepsilon(z_\text{train}) \;=\; \arg\min_{\theta}\;R_\varepsilon(\theta, z_\text{train})\]

Ce qui revient à chercher les $\theta_\varepsilon(z_\text{train})$ dont le gradient de cette nouvelle loss en $\theta$ est nul , car $\theta_\varepsilon(z_\text{train})$ est un minimum local de $R_\varepsilon$ si et seulement si (si la fonction est convexe: mais pas le cas pour les réseaux de neurone, cf partie 1.3.2) sa dérivée première (gradient) s’annule:

\[\nabla_\theta R_\varepsilon\bigl(\theta_\varepsilon(z_\text{train})\bigr) = 0.\]

1.1.2.2. Approximation de Taylor à l’ordre 1 en $\varepsilon = 0$ de $\theta_\varepsilon$

Pour cette partie, on écrit pour simplifier $\theta_\varepsilon$ au lieu de $\theta_\varepsilon(z_\text{train})$

En développant à l'aide de l'approximation de Taylor en $\hat{\theta}$ pour un tout petit $\varepsilon$, ie proche de 0, donc pour un $\theta_\varepsilon$ proche de $\hat{\theta}$, cette formule:

\[\frac{1}{n}\sum_{i=1}^n \nabla_\theta \mathcal{L}(z_i,\theta_\varepsilon) \;+\;\varepsilon\,\nabla_\theta \mathcal{L}(z_{\rm train},\theta_\varepsilon)\]

Rappel de la formule de Taylor à l’ordre 1 en $\varepsilon = 0$:

\[f(\theta_\varepsilon) \approx f(\hat{\theta}) + f'(\hat{\theta})\,(\theta_\varepsilon - \hat{\theta})\]

On obtient :

\[\begin{split} \nabla_\theta R_\varepsilon\bigl(\theta_\varepsilon\bigr) &= \underbrace{\frac{1}{n}\sum_{i=1}^n \nabla_\theta \mathcal{L}(z_i,\theta_\varepsilon) \;+\;\varepsilon\,\nabla_\theta \mathcal{L}(z_{\rm train},\theta_\varepsilon)}_{f(\theta_\varepsilon)} \\ &\approx \underbrace{[ \frac{1}{n}\sum_{i=1}^n \nabla_\theta \mathcal{L}(z_i,\hat{\theta}) \;+\;\varepsilon\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) ]}_{f(\hat{\theta})} \;\; + \;\; \underbrace{[ \frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta}) \;+\;\varepsilon\,\nabla^2_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) ]}_{f'(\hat{\theta}) = \nabla_\theta f(\hat{\theta})} \;\;(\theta_\varepsilon - \hat{\theta}) \end{split}\]

\(\nabla_\theta R_\varepsilon\bigl(\theta_\varepsilon\bigr) = 0\) nous ramène donc à la formule:

\[\left[ \frac{1}{n}\sum_{i=1}^n \nabla_\theta \mathcal{L}(z_i,\hat{\theta}) + \varepsilon\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \right] + \left[ \frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta}) + \varepsilon\,\nabla^2_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \right] \; \; (\theta_\varepsilon - \hat{\theta}) \; \; \approx 0\]

D’où, en isolant $(\theta_\varepsilon - \theta)$ dans l’équation:

\[\theta_\varepsilon - \hat{\theta} \approx - \left[ \frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta}) + \varepsilon\,\nabla^2_\theta \mathcal{L}(z_{\rm train},\hat{\theta}(z_\text{train})) \right]^{-1} \;\; \times \;\; \left[ \frac{1}{n}\sum_{i=1}^n \nabla_\theta \mathcal{L}(z_i,\hat{\theta}) + \varepsilon\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \right]\]

Or, puisque $\hat{\theta}$ sont les poids optimaux pour le modèle de base, $\frac{1}{n}\sum_{i=1}^n \nabla_\theta \mathcal{L}(z_i,\hat{\theta}) = 0$:

\[\theta_\varepsilon - \hat{\theta} \approx - \left[ \frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta}) + \varepsilon\,\nabla^2_\theta \mathcal{L}(z_{\rm train},\hat{\theta}(z_\text{train})) \right]^{-1} \;\; \times \;\; \varepsilon\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta})\]

1.1.2.3. $\theta_\varepsilon - \theta$ donne un terme en fonction de $\varepsilon$ x une série en $\varepsilon$: on va montrer qu’on ne peut garder que la constante (indépendante de $\varepsilon$) de la série à l’ordre 1

Ici, on a :

\[\theta_\varepsilon - \hat{\theta} \approx - \left[ \underbrace{\frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta})}_{= a} + \varepsilon\,\underbrace{\nabla^2_\theta \mathcal{L}(z_{\rm train},\hat{\theta}(z_\text{train}))}_{= b} \right]^{-1} \;\; \times \;\; \varepsilon\,\underbrace{\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta})}_{= \beta}\]

On sait que $A(I-A)^{-1}$ peut se ramener à une somme : $A(I-A)^{-1} = \sum_{i=0}^{\inf}{A^i}$ => cf ce post de blog ou cf les séries de Neumann.

Du coup on a $(a + \varepsilon b)^{-1}$ qui peut se ramener à quelque chose de la forme :

A COMPLETER!!!

En gros, l’idée c’est qu’on obtient qqch du genre: \(\begin{split} (a + \varepsilon b) \times \varepsilon \beta &= \varepsilon \beta a + \varepsilon^2 b \beta \\ &\underbrace{\approx}_{\text{à l'ordre 1}} \varepsilon \beta a \end{split}\)

Et que les termes en $\varepsilon ^2$ sont négligeables puisqu’on fait une approximation pour $\varepsilon$ proche de 0 à l’ordre 1.

En gros, on se retrouve avec:

\[\colorbox{orange}{$\displaystyle(\theta_\varepsilon - \theta)$} \approx - [\frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta})]^{-1} \times \colorbox{cyan}{$\displaystyle \varepsilon $} \,\colorbox{pink}{$\displaystyle \nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) $}\]

Et si on dérive par rapport à $\varepsilon$ on obtient:

\[\begin{split} \frac{d}{d \colorbox{cyan}{$\displaystyle \varepsilon $}}\colorbox{orange}{$\displaystyle(\theta_\varepsilon - \theta)$} &= \colorbox{yellow}{$\displaystyle \frac{d}{d\varepsilon} \theta_\varepsilon $} \\ &\approx - [\underbrace{\frac{1}{n}\sum_{i=1}^n \nabla^2_\theta \mathcal{L}(z_i,\hat{\theta})}_{\colorbox{red}{$\displaystyle H_\theta (\hat{\theta}) $}}]^{-1} \times \colorbox{pink}{$\displaystyle \nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta})$} \\ &\approx - \colorbox{red}{$\displaystyle H_\theta (\hat{\theta}) $}^{-1} \nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \end{split}\]

D’où :

\[\colorbox{yellow}{ $\displaystyle \frac{d}{d\varepsilon} \theta_\varepsilon(z_\text{train}) = - H_\theta^{-1}(\hat{\theta}) \nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) $}\]

Ainsi, quand on multiplie par $\nabla_\theta \,\mathcal{L}\bigl(z_{\mathrm{test}},\,\hat{\theta}\bigr)$ on obtient a la formule de l’influence:

\[\begin{split} \mathrm{Influence}\bigl(z_{\mathrm{train}}\to z_{\mathrm{test}}\bigr) &= I_{z_\text{test}}\bigl(z_{\mathrm{train}}\bigr) \\ &= \frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\ \theta_\varepsilon(z_\text{train})\bigr) \Big|_{\varepsilon=0} \\ &= -\nabla_\theta \,\mathcal{L}\bigl(z_{\mathrm{test}},\,\hat{\theta}\bigr)H_\theta^{-1}(\hat{\theta})\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta}) \end{split}\]

ou:

\[\begin{split} \mathrm{Influence}\bigl(z_{\mathrm{train}}\to f(x)\bigr) &= I_{f(x)}(z_{\mathrm{train}}) \\ &= \left.\frac{d}{d\varepsilon}\bigl(f_{\theta_{\varepsilon}(z_{\mathrm{train}})}(x)\bigr)\right|_{\varepsilon=0} \\ &= - \nabla_\theta f_{\hat{\theta}}(x)^\top \, H_\theta(\hat{\theta})^{-1} \, \nabla_\theta \mathcal{L}\bigl(z_{\mathrm{train}},\hat{\theta}\bigr) \end{split}\]

1.2 “Corrections” des fonctions d’influence

Beaucoup de correction du calcul de l’influence sont mises en places pour les modèles de deep learning:

1.2.1. Hesienne pas forcément inversible…

Dans les réseaux de neurones, la loss d’entraînement n’est pas fortement convexe (le minimum local n’est pas forcément un minimum global…) donc la hessienne peut être non inversible. Donc, des approches ont été étudiées pour garantir l’inversibilité de la hessienne, en ajoutant notamment un terme dit de “damping” $\lambda >0$.

1.2.2. Hessienne par rapport aux paramètres du réseau compliquée à calculer pour des réseaux avec un grand nombre de paramètres…

1.2.2.1. Approximation par la hessienne de Gauss-Newton (Fisher Information Matrix)

Le papier If Influence Functions are the Answer, Then What is the Question? propose d’approximer la Hessienne par la Hessienne de Gauss–Newton (GNH), notée $G_\theta$ :

\[G_\theta = J_{y\theta}^T \, H_y \, J_{y\theta}\]

où :

• $J_{y\theta}$ est la matrice Jacobienne des sorties du réseau par rapport aux paramètres ;
• $H_y = \nabla^2_y \mathcal{L}(y, \theta)$ est la Hessienne de la fonction de coût par rapport aux sorties du réseau. propose d’approximer la Hessienne par la matrice d’information de Fisher (équivalente à la Hessienne de Gauss-Newton).

En fait, on a:

\[\underbrace{H_\theta}_{\text{Très difficile}} =\;\;\; \underbrace{J_{y\theta}^T \, H_y \, J_{y\theta}}_{\text{Facile (GNH)}} \;\;\;+ \underbrace{\sum_i \frac{\partial \mathcal{L}}{\partial y_i} \,\nabla_\theta^2 y_i}_{\text{Cauchemar computationnel}}\]

avec:

• $J_{y\theta}$ : Déjà calculé par backpropagation standard
• $H_y$ : Matrice $k \times k$ avec $k =$ le nombre de tokens possibles (ex : 151936 pour Qwen)

On va essayer de décortiquer la hessienne pour retrouver cette formule:

\[H_\theta = \frac{\partial ^2 \mathcal{L}}{\partial \theta}\]

Or, par chain rule, avec $\mathcal{L}$ qui est une fonction de perte (loss) qui dépend de la sortie du modèle $y$, $y$ qui est la sortie du modèle, qui dépend des paramètres du modèle $\theta$, d’où on a: \(\mathcal{L} = \mathcal{L}(y(\theta))\)

Rappel: \(\frac{\partial}{\partial x} f(g(x)) = f'(g(x)) \cdot g'(x)\)

D’où:

\[\frac{\partial \mathcal{L}}{\partial \theta} = \frac{\partial \mathcal{L}}{\partial y} \cdot \frac{\partial y}{\partial \theta}\]

Ainsi:

\[\begin{split} \frac{\partial ^2 \mathcal{L}}{\partial \theta} &= \frac{\partial}{\partial \theta} (\frac{\partial \mathcal{L}}{\partial \theta}) \\ &= \frac{\partial}{\partial \theta} (\frac{\partial \mathcal{L}}{\partial y} \cdot \frac{\partial y}{\partial \theta}) \end{split}\]

Par dérivée d’une multiplication de fonctions : Rappel: \((f \times g)' = f'g + g'f\)

Avec

• \[f = \frac{\partial \mathcal{L}}{\partial y}\]
• \[g = \frac{\partial y}{\partial \theta}\]

On a:

\[\begin{split} H_\theta &= \frac{\partial ^2 \mathcal{L}}{\partial \theta} \\ &= \frac{\partial}{\partial \theta} (\frac{\partial \mathcal{L}}{\partial y} \times \frac{\partial y}{\partial \theta}) \\ &= \colorbox{lime}{$\displaystyle \underbrace{\frac{\partial}{\partial \theta} (\frac{\partial \mathcal{L}}{\partial y})}_{= f'}$} \times \colorbox{pink}{$\displaystyle \underbrace{\frac{\partial y}{\partial \theta}}_{= g} $} \;\; + \;\; \colorbox{brown}{$\displaystyle \underbrace{\frac{\partial}{\partial \theta} (\frac{\partial y}{\partial \theta})}_{= g' = \frac{\partial ^2 y}{\partial \theta ^2} = \nabla ^2_\theta y} \times \underbrace{\frac{\partial \mathcal{L}}{\partial y}}_{= f}$} \end{split}\]

Concentrons-nous sur \(\frac{\partial}{\partial \theta} (\underbrace{\frac{\partial \mathcal{L}}{\partial y}}_{= h})\):

Par chain rule (car la dérivée de $h$ qu’on cherche dépend d’une variable intermédiaire (ici $y$), qui dépend elle-même de $\theta$)

\[\begin{split} \colorbox{lime}{$\displaystyle \frac{\partial}{\partial \theta} \left( \frac{\partial \mathcal{L}}{\partial y} \right) $} &= \frac{\partial h}{\partial y} \cdot \frac{\partial y}{\partial \theta} \\ &= \frac{\partial}{\partial y} (\frac{\partial \mathcal{L}}{\partial y}) \cdot \frac{\partial y}{\partial \theta} \\ &= \underbrace{\frac{\partial^2 \mathcal{L}}{\partial y^2}}_{= H_y} \cdot \underbrace{\frac{\partial y}{\partial \theta}}_{= J_{y \theta}} \\ \end{split}\]

On se retrouve donc avec: \(H_\theta = \colorbox{pink}{$\displaystyle J_{y\theta}^T $} \, \colorbox{lime}{$\displaystyle H_y \, J_{y\theta} $} + \colorbox{brown}{$\displaystyle \nabla_\theta^2 y \cdot \frac{\partial \mathcal{L}}{\partial y}$}\)

Ainsi, afin de ne pas calculer les dérivées secondes à travers tout le réseau (ce qui est très coûteux quand on a beaucoup de paramètres), on utilise, pour l’ensemble des calculs d’influence (surtout pour les LLMs), ce résultat:

\[H_\theta^{-1}(\hat{\theta})\approx \bigl(G_\theta + \lambda I\bigr)^{-1}.\]

On va voir pourquoi on peut écrire:

\[\boxed{ \underbrace{\mathbb{E}[H_\theta]}_{\text{très difficile à calculer}} \;\approx\; \underbrace{\mathbb{E}[J_{y\theta}^\top \, H_y \, J_{y\theta}]}_{\text{Gauss--Newton (plus simple)}} \;\approx\; \underbrace{\mathbb{E}[\nabla_\theta \ell(z, \theta)\, \nabla_\theta \ell(z, \theta)^\top]}_{\text{On va montrer ça, c'est ce qui est utilisé dans KFAC}}, }\]

Note qu’on appelle pour simplifier: \(g = \nabla_\theta \ell\;\\ g^\top = \nabla_\theta \ell^\top\)

Donc ce qu’on utilise dans KFAC, concrètement, c’est :

\[\boxed{ \mathbb{E}[H_\theta] \;\approx\; \mathbb{E}[gg^\top] }\]

Détail de cette égalité:

Comme vu précédemment, le gradient par rapport aux paramètres s’écrit :

\[\nabla_\theta \ell = J_{y\theta}^\top \, \nabla_{\hat y} \ell,\]

où :

\[J_{y\theta} = \frac{\partial \hat y}{\partial \theta}, \qquad \nabla_{\hat y} \ell = \frac{\partial \ell}{\partial \hat y}.\]

D’où :

\[\boxed{ \begin{aligned} \nabla_\theta \ell \, \nabla_\theta \ell^\top &= \left(J_{y\theta}^\top \nabla_{\hat y} \ell\right) \left(\nabla_{\hat y} \ell^\top J_{y\theta}\right) \\ &= J_{y\theta}^\top \left( \nabla_{\hat y} \ell \, \nabla_{\hat y} \ell^\top \right) J_{y\theta} \end{aligned} }\]

Or, fonction de loss de type negative log-likelihood (comme c’est le cas pour les llms) :

\[\ell(y,\hat y) = -\log p_\theta(y \mid x),\]

on a l’identité statistique suivante :

\[\mathbb{E}\!\left[ \nabla_{\hat y} \ell \; \nabla_{\hat y} \ell^\top \right] = \mathbb{E}\!\left[ H_y \right],\]

D’où: \(\boxed{ \begin{aligned} & \mathbb{E}[J_{y\theta}^\top \left( \nabla_{\hat y} \ell \, \nabla_{\hat y} \ell^\top \right) J_{y\theta}] \\ \; &\approx\; \mathbb{E}[J_{y\theta}^\top \, H_y \, J_{y\theta}] \end{aligned} }\)

1.2.2.2. Factorisation par blocs de $G_\theta$ et factorisation en produit de Kronecker pour pourvoir stocker cette matrice & paralléliser les calculs entre couches

Au lieu d’inverser directement la grande matrice $\,G_\theta+\lambda I$, le papier Scalable Multi-Stage Influence Function for Large Language Models via Eigenvalue-Corrected Kronecker-Factored Parameterization exploite sa structure en blocs correspondant à chaque couche du réseau.

\[G = \begin{bmatrix} G_{1,1} & G_{1,2} & \cdots\\ G_{2,1} & G_{2,2} & \\ \vdots & & \ddots \end{bmatrix},\]

Pour un réseau à $L$ couches, on a donc \(G = [G_{i,j}]_{1 \leq i, j \leq L}\), avec \(G_{i,j}\) qui représente le bloc entre les paramètres de la couche $i$ et de la couche $j$.

Cette séparation en bloc permet au papier de simplifier $G$ en ne gardant que les blocs diagonaux :

\[G \approx \tilde{G} = \mathrm{diag}(G_{1,1}, G_{2,2}, \dots, G_{L,L})\]

Cela signifie qu’on ignore les interactions entre différentes couches et qu’on ne considère que les blocs $G_{l,l}$ pour chaque couche $l$.

Cette approche par blocs permet :

• De traiter chaque couche indépendamment
• D’éviter de stocker/calculer la matrice complète de taille $p \times p$ (où $p$ est nombre total de paramètres)
• De paralléliser les calculs entre couches

C’est ce qui rend la méthode scalable pour les grands modèles comme les LLMs avec des milliards (plutôt même billions…) de paramètres.

Calcul du gradient bloc par bloc

Concrètement, dans K-FAC, on introduit un autre gradient, local à la couche $i$. En gros, normalement on fait:

\[\mathbb{E}[H_\theta] \;\approx\; \mathbb{E}[\nabla_\theta \ell(z, \theta)\, \nabla_\theta \ell(z, \theta)^\top]\]

Mais ici, on ne considère les éléments que couches par couches, donc on restreint les poids $\theta$ à une couche $i$. En gros, on regarde le bloc de la Fisher correspondant aux paramètres de la couche $i$ :

\[\mathbb{E}[H_{\theta_i}] \;\approx\; \mathbb{E}[\nabla_{\theta_i} \ell(z, \theta)\, \nabla_{\theta_i} \ell(z, \theta)^\top]\]

Or, si $W_i$ est la matrice de paramètres d’une couche dense du réseau: \(\nabla_{\theta_i} \ell(z, \theta) = \text{vec}(\nabla_{W_i} \ell(z, \theta))\)

Or, pour une couche dense:

\[\nabla_{W_i} \ell(z, \theta) = \nabla_{h_i} \ell(z, \theta) a_i^\top\]

Avec $h_i$ les pré-activations de la couche $i$ car on applique une chain rule avec $ h_i = W_i a_i + b_i$ pour une couche dense.

Si on transforme en vecteur, cela revient à: \(\mathrm{vec}\!\left(\nabla_{W_i}\ell\right) = a_i \otimes \nabla_{h_i}\ell\)

Donc pour chaque couche $i$ on calcule $a_i \otimes \nabla_{h_i}\ell$

On nomme $G_i = \nabla_{h_i}\ell$.

Comment représenter ça dans le code?

Dans le code, pour représenter une couche dense avec biais, on représente le bloc de paramètres comme une matrice augmentée :

\[W' = \begin{bmatrix} W \\ b^\top \end{bmatrix} \in \mathbb{R}^{(d_{\text{in}} + 1)\times d_{\text{out}}}\]

Terme de damping: approximation factorisée

Rappelons que nous avons besoin d’un terme de damping $\delta$ afin de stabiliser l’inversion. C’est encore plus le cas ici avec le produit de Kronoeker car il amplifie les petites valeurs propres avec la multiplication. Le papier Optimizing Neural Networks with Kronecker-factored Approximate Curvature propose un $\pi$-damping. On définit le coefficient de répartition du damping pour la couche $i$ comme : \(\pi_i = \sqrt{ \frac{\operatorname{tr}(A_i)/\dim(A_i)} {\operatorname{tr}(G_i)/\dim(G_i)} }\) En effet, normalement le damping est : $G_i \otimes A_i + \delta I$. Cependant, cette expression ne peut pas être factorisée exactement sous la forme $(G_i + \delta I) \otimes (A_i + \delta I)$. K-FAC introduit donc une approximation factorisée du damping :

\[G_i \otimes A_i + \delta I \;\approx\; (G_i + \tfrac{\sqrt{\delta}}{\pi_i} I) \;\otimes\; (A_i + \sqrt{\delta}\,\pi_i I)\]

Le rôle de $\pi_i$ est alors de répartir le damping entre $A_i$ et $G_i$ de manière équilibrée. On utlise la trace car our une matrice symétrique définie positive $M$, la trace vérifie $\operatorname{tr}(M) = \sum_k \lambda_k$ où $\lambda_k$ sont les valeurs propres de $M$, ainsi la quantité $\frac{\operatorname{tr}(M)}{\dim(M)}$ correspond à correspond à une estimation de l’échelle spectrale moyenne de $M$. Les valeurs propres du produit de Kronecker sont : $\lambda_{jk} = \lambda_j^{G_i}\,\lambda_k^{A_i}$. Si $A_i$ et $G_i$ ont des échelles très différentes, le produit peut être très mal conditionné. Le coefficient $\pi_i$ est choisi de sorte que, en moyenne, le damping appliqué à $A_i$ et à $G_i$ ait un effet comparable sur ces valeurs propres.

Si $A_i$ et $G_i$ ont des échelles très différentes, le produit peut être très mal conditionné. Le coefficient $\pi_i$ est choisi de sorte que, en moyenne, le damping appliqué à $A_i$ et à $G_i$ ait un effet comparable sur ces valeurs propres.

En imposant un équilibrage de premier ordre entre les termes croisés du produit factorisé, on obtient : \(\pi_i^2 = \frac{\operatorname{tr}(A_i)}{\operatorname{tr}(G_i)} \cdot \frac{\dim(G_i)}{\dim(A_i)}\)

Diagonalisation de $A_i \otimes G_i$ pour l’inversion

Pour inverser $A_i \otimes G_i$ on va diagonaliser $A_i \otimes G_i$ se ramener à $(G \otimes A + \delta I)^{-1}= Q \Lambda^{-1} Q^\top$ avec: \(\Lambda^{-1} = \operatorname{diag}\!\left( \frac{1}{\lambda_1}, \frac{1}{\lambda_2}, \ldots \right)\)

et $\lambda_k$ les valeurs propres de $G \otimes A + \delta I$.

1.2.2.2.3. EK-FAC

1.2.3. Données d’entraînement mal apprises prédominantes: comment corriger?

A noter que le papier Influence Functions in Deep Learning Are Fragile indique que les fonctions d'influence sont biaisées vers les exemples à forte perte. en effet, le gradient de la loss des points d'entraînement est plus élevé pour les exemples mal appris, entraînant un biais systématique vers ces exemples dans l’attribution d’influence, indépendamment de leur véritable effet sur la fonction qu'on veut mesurer ou sur la loss sur notre $z_\text{test}$. Le papier RelatIF: Identifying Explanatory Training Examples via Relative Influence propose de recalculer les scores d’influence en normalisant l'influence par l'inverse de la hessienne x le gradient de la loss du training datapoint, éliminant ainsi les gradients élevés pour des exemples mal appris par le modèle (sans lien avec la fonction à maximiser).

\[\begin{split} \mathrm{Influence}\bigl(z_{\mathrm{train}}\to z_{\mathrm{test}}\bigr) &= \frac{\frac{d}{d\varepsilon} \mathcal{L}\bigl(z_{\rm test},\theta_\varepsilon(z_\text{train})\bigr)}{||H_\theta^{-1}(\hat{\theta}) \;\; \nabla_\theta \mathcal{L}(z_\text{test}, \hat{\theta})||} \Big|_{\varepsilon=0} \\ &= \frac{-\nabla_\theta \,f(\theta_\varepsilon(z_\text{train}))H_\theta^{-1}(\hat{\theta})\nabla_\theta \mathcal{L}(z_{\rm train},\theta_\varepsilon(z_\text{train}))}{||H_\theta^{-1}(\hat{\theta}) \;\; \nabla_\theta \mathcal{L}(z_\text{test}, \hat{\theta})||} \end{split}\]

1.3. Le cas des LLMs: besoin d’une influence token-wise ou sentence-wise

Le papier Studying Large Language Model Generalization with Influence Functions présente l’application des fonctions d’influence aux LLMs. Dans le cas des LLMs, la loss est la negative log-vraisemblance. La première particularité d'un LLM, c'est le fait qu'un datapoint est un peu compliqué à définir. On peut supposer qu'il s'agit d'une phrase (et son label, le token suivant la phrase), ou on peut considérer le token lui-même (l’input étant la phrase le précédent, le label le token en question, par exemple). Mais il est important de bien définir de quoi on parle quand on parle de “datapoint”.

1.3.1 L’influence à l’échelle de la phrase $z_m$

Supposons que $z_m$ soit cette phrase “le chat est gris”, soit ce datapoint:

\[[\text{BOS, le, chat, est, gris}] \rightarrow \text{[EOS]}\]

Vu qu’on est dans un cas autorégressif (c’est-à-dire que les tokens sont prédits à partir des tokens précédents de la séquence) :

Si \(z_m\) de taille \(T\) :

\[\nabla_\theta L(z_m, \theta) = \sum_{t=1}^T(-\nabla_\theta \log p(z_{m,t} \mid z_{m, \lt t}, \theta))\]

Nous, \(z_m\) est de taille 6 :

\[\begin{split} \nabla_\theta L(z_m, \theta) &= -\nabla_\theta \log p(\text{le} \mid \text{[BOS]}, \theta) \\ &\quad - \nabla_\theta \log p(\text{chat} \mid \text{[[BOS], le]}, \theta) \\ &\quad - \nabla_\theta \log p(\text{est} \mid \text{[BOS], le, chat}, \theta) \\ &\quad - \nabla_\theta \log p(\text{gris} \mid \text{[BOS], le, chat, est}, \theta) \\ &\quad - \nabla_\theta \log p(\text{[EOS]} \mid \text{[BOS], le, chat, est, gris}, \theta) \end{split}\]

1.3.2 L’influence à l’échelle des tokens $t\;\;$ dans la phrase $z_m$

On peut aussi considérer l’échelle du token, comme on l’a mis plus haut, en considérant l’input comme étant la phrase précédant ce token, et le label ce token en question.

On a ici $\nabla_\theta L(z_m, \theta)$ qui est la somme des gradients de la loss au niveau de chaque token. Du coup, il suffit de prendre $- \nabla_\theta \log p(\text{gris} \mid \text{[BOS], le, chat, est}, \theta)$ pour avoir l’influence du token gris dans la séquence par exemple. On peut ainsi avoir l’information token par token.

Et ça c’est ce qu’on obtient ici (cf Studying Large Language Model Generalization with Influence Functions, Grosse 2023) :

\[\nabla_\theta L(\text{token t dans } z_m, \theta) = \nabla_\theta \log p(\text{token t} \mid \text{ce qui est avant token t dans } z_m, \theta)\]

On obtient donc la formule:

\[I_f(z_{m,t}) = \nabla_{\theta}f_{\theta_\varepsilon(z_\text{train})}(x)^{T} H^{-1} \nabla_{\theta}\log p(z_{m,t}\mid z_{m,\lt t}, \theta)\]

Prenons l’exemple suivant: on prend $f = \log p(\text{“hydrogen and oxygen”} \mid \text{“Water is composed of”})$ et $z_m$ qui est le texte ci-dessous. On peut afficher l’influence token par token dans le texte:

1.4 Le cas des LLMs: beaucoup de données d’entraînement (eg. 36 trillions de tokens pour Qwen3) => query batching ou semantic matching pour ne pas calculer l’influence sur toutes les données (trop coûteux)

Le papier Studying Large Language Model Generalization with Influence Functions propose une approche pour éviter de calculer les gradients de tous les exemples d’entraînement candidats pour chaque requête d’influence. Pour cela, ils “filtrent” les données d’entraînement par rapport à la phrase test via un filtrage TF-IDF et une approche qu’ils introduisent de “query batching”.

1.4.1 Le filtrage TF-IDF

Le filtrage TF-IDF utilise une technique classique de recherche d’information pour présélectionner les séquences d’entraînement les plus susceptibles d’être influentes. L’intuition derrière est que les séquences pertinentes devraient avoir au moins un certain chevauchement de tokens avec la requête.

Ils retiennent les top 10,000 séquences selon le score TF-IDF Calcul d’influence et calculent les influences uniquement sur ces séquences présélectionnées.

1.4.2 Le Query-Batching

Dans un LLM, on a beaucoup d’exemples $z_m$ d’entraînement. Donc, on calcule séparemment $\nabla_\theta\mathcal{L}(z_m, \theta_\varepsilon(z_\text{train}))$ et $\nabla_{\theta} f(\theta_\varepsilon(z_\text{train}))^\top \, H^{-1}$ qui se calcule en une fois.

Pour stocker de nombreux gradients de requêtes en mémoire ($\nabla_\theta\mathcal{L}(z_m, \theta_\varepsilon(z_\text{train})) \; \forall \; z_m$), ils approximent chaque matrice de gradient préconditionné comme étant de rang faible (rank-32 dans leurs expériences).

Ainsi, pour chaque requête, ils n’ont pas à refaire les calculs! Ils ont juste à calculer $\nabla_{\theta} f(\theta_\varepsilon(z_\text{train}))$.

1.5 Le cas des LLMs: plusieurs couches d’entraînement (pretraining, fine-tuning, alignement, …) => multi-stage influence functions

Le papier Scalable Multi-Stage Influence Function for Large Language Models via Eigenvalue-Corrected Kronecker-Factored Parameterization explique que la fonction d’influence classique $I_f(z_{m,t}) = \nabla_{\theta}f_{\theta_\varepsilon(z_\text{train})}(x)^{T} H^{-1} \sum_{t=1}^T(-\nabla_\theta \log p(z_{m,t} \mid z_{m, <t}, \theta))$ permet de quantifier l’impact d’une phrase d’entraînement sur les prédictions du modèle. Cependant, on a des modèles qui sont passés par plusieurs phases d’entraînement pour les LLMs (avec plusieurs données différentes). En effet, les LLMs sont pré-entraînés (modèles “base”), puis instruct-tuné (modèles “chat”), puis passent par du reinforcement learning (ou du “faux” réinforcement learning (DPO, …)) pour la phase d’alignement. Donc notre formule ne marche plus si on prend un modèle “chat” par exemple (les 3/4 des modèles qu’on trouve sur huggingface) et qu’on veut calculer l’influence d’une phrase du jeu de pre-entraînement par exemple. Or, ce sont ces données de pré-entraînement qui nous intéressent puisque la majorité des connaissances d’un LLM sont acquises pendant le pré-entraînement. Sans pouvoir les tracer, on ne peut pas expliquer d’où viennent les réponses du modèle.

Ainsi, les auteurs du papier proposent une connexion entre l’espace des paramètres du modèle pré-entraîné et celui du modèle fine-tuné. L’intuition est que le fine-tuning ne devrait pas trop éloigner les paramètres de leur état pré-entraîné. On reformule donc l’objectif de fine-tuning avec une contrainte de proximité euclidienne :

\[\theta^{ft} = \arg\min_\theta \mathcal{L}_{ft}(\theta) + \frac{\alpha}{2}||\theta - \theta^{pt}||_2^2\]

où :

• $\mathcal{L}_{ft}(\theta)$ est la loss de fine-tuning
• $\alpha \in \mathbb{R}^+$ est un hyperparamètre contrôlant la proximité
• \(\|\theta - \theta^{pt}\|_2^2\) est la distance euclidienne entre les paramètres du modèle pré-entraîné avec le modèle fine-tuné (final)

Avec cette reformulation, on peut dériver la fonction d’influence multi-étapes :

\[I_f(z_m) = \nabla_\theta f(\theta^{ft})^T \left(\nabla^2_\theta \mathcal{L}_{ft}(\theta^{ft}) + \alpha I\right)^{-1} \left(\nabla^2_\theta \mathcal{L}_{pt}(\theta^{pt})\right)^{-1} \nabla_\theta \mathcal{L}(z_m, \theta^{pt})\]

Ainsi, on a 2 hessiennes:

• Hessienne du pré-entraînement : \(\left(\nabla^2_\theta \mathcal{L}_{pt}(\theta^{pt})\right)^{-1}\)
  • Calculée aux paramètres $\theta^{pt}$ (modèle pré-entraîné)
  • Capture la courbure de la loss de pré-entraînement
• Hessienne du fine-tuning : \(\left(\nabla^2_\theta \mathcal{L}_{ft}(\theta^{ft}) + \alpha I\right)^{-1}\)
  • Calculée aux paramètres $\theta^{ft}$ (modèle fine-tuné)
  • Inclut le terme de régularisation $\alpha I$ qui encode la contrainte de proximité

Cette double inversion de Hessienne permet de :

• Première inversion : Transformer le gradient de l’exemple de pré-entraînement en changement de paramètres
• Seconde inversion : Propager ce changement à travers le fine-tuning pour voir son impact final

C’est comme si on “remontait” l’influence à travers deux étapes d’entraînement successives.

1.6 Beaucoup de sujets récents de recherche utilisent les fonctions d’influence pour déterminer les données utiles (qu’on peut utiliser pour fine-tuner le modèle) pour améliorer la génération d’un LLM, ou ajouter une “connaissance” au modèle par exemple

Les fonctions d’influence sont un bon moyen d’évaluer l’impact de chaque exemple de données sur les performances d’un LLM dans un domaine donné. Pour l’instruction-tuning, elles permettent de mesurer précisément quels couples question-réponse contribuent le plus à la qualité des réponses générées dans un domaine donné. Pour le continual pretraining, elles identifient les phrases dont l’ajout ou la suppression modifie le plus la capacité du modèle à maîtriser un vocabulaire ou un style spécifique. Les fonctions d’influence sont de plus en plus utilisées pour affiner le corpus d’apprentissage et maximiser le gain de performance du LLM sur un domaine cible. Voici quelques exemples de papier faisant cela:

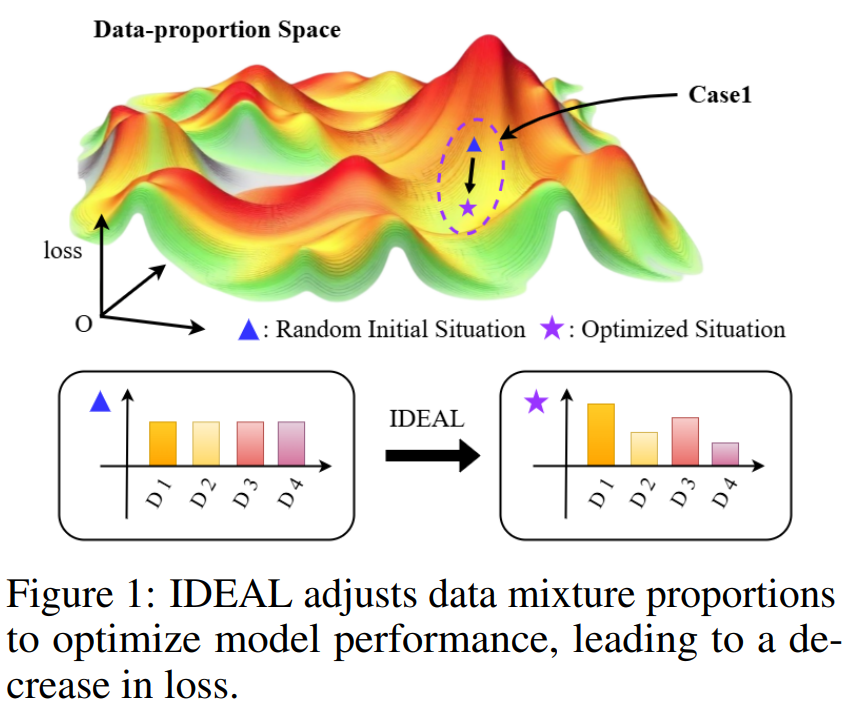
IDEAL: Data Equilibrium Adaptation for Multi-Capability Language Model Alignment

Cliquez pour voir l’illustration IDEAL

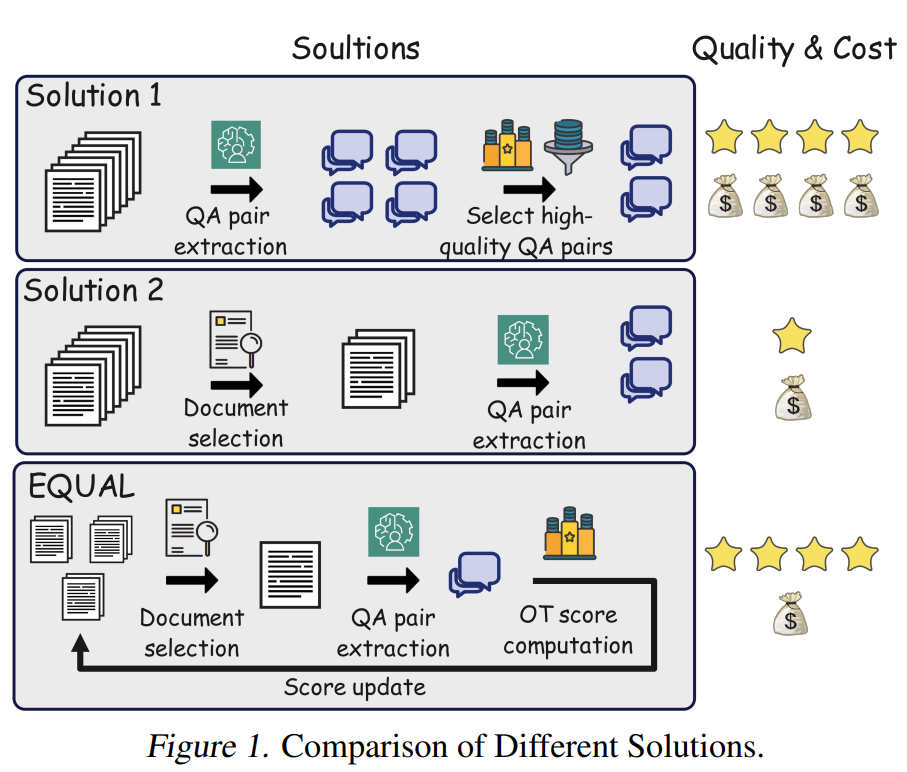
Not All Documents Are What You Need for Extracting Instruction Tuning Data

Cliquez pour voir l’illustration de EQUAL