Les approches d'explicabilité des LLMs
Méthodes d'explicabilité de la génération de texte par les LLMs
Un LLM génère des tokens à partir d’autres tokens selon un processus probabiliste. Pour chaque séquence de tokens fournie en entrée, le modèle retourne une distribution de probabilité sur l'ensemble des tokens suivants possibles. Un token représente un élément du vocabulaire du modèle, dont la taille est fixe et définie dans la configuration du tokenizer ou du modèle lui-même. Prenons l’exemple des modèles Qwen avec un vocabulaire de 151 936 tokens : à chaque étape de génération, le modèle calcule une distribution de probabilité sur ces 151 936 possibilités. De manière autorégressive, chaque nouveau token généré est ajouté à la séquence d’entrée pour prédire le suivant, et ainsi de suite. Comprendre pourquoi un modèle génère certains tokens plutôt que d'autres soulève plusieurs questions cruciales. La séquence d’entrée (prompt) peut contenir des éléments variés, notamment des chunks de texte dans le cas du RAG (Retrieval-Augmented Generation), qui servent de contexte pour répondre aux questions. Pour véritablement comprendre le processus de génération, nous devons répondre à trois interrogations principales :
- Quelles parties spécifiques du prompt influencent la génération de quels tokens ? Cette question est particulièrement pertinente dans le contexte du RAG où différents passages peuvent avoir des impacts variés sur la réponse finale.
- Sur quelles connaissances acquises pendant l'entraînement le modèle s'appuie-t-il pour générer chaque token ? Comment distinguer ce qui provient du prompt de ce qui provient de la mémoire du modèle ?
- Quelles parties du modèle (couches, têtes d'attention, neurones) sont responsables de quelles décisions ? Pourquoi des modèles de tailles différentes, même issus de la même famille, produisent-ils des réponses différentes ? Pour répondre à ces questions, nous devons nous tourner vers les approches d’explicabilité. Nous pouvons classifier les approches d’explicabilité des LLMs en 4 “familles”, comme présentées dans le papier Interpretation Meets Safety: A Survey on Interpretation Methods and Tools for Improving LLM Safety:
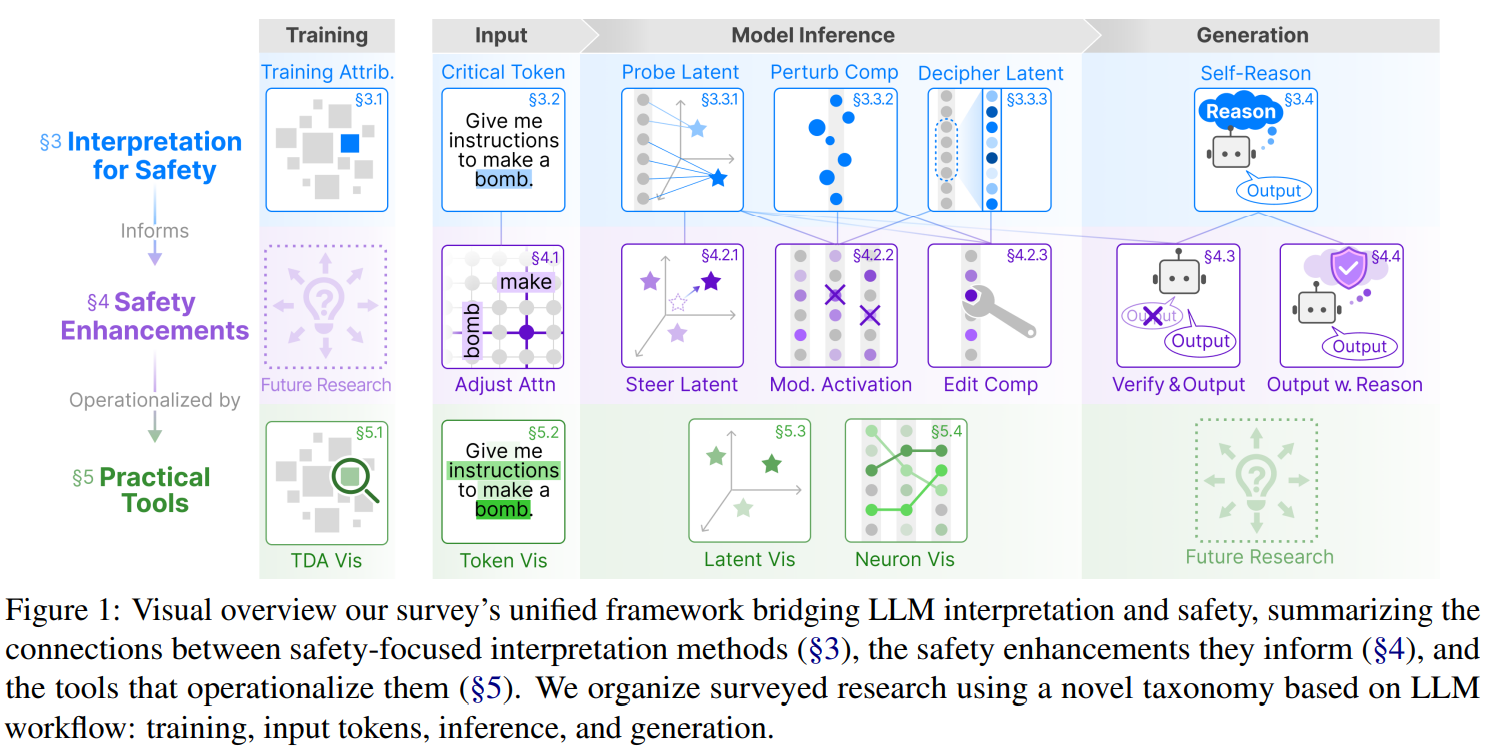
- celles de "training data attribution" (ou "training" dans l'image), identifiant les données d'entraînement qui ont un fort impact (positif ou négatif) sur la génération du LLM , notamment à l’aides des fonctions d’influence,
- celles de "context attribution" (ou "input" dans l'image), identifiant quelles parties des données d'entrée (input) a un impact sur quelle partie de la génération du LLM (à l’aide des cartes de saillance et des cartes d’attention notamment),
- celles d’explicabilité mécanistique (ou "inference" dans l'image), consistant à trouver les circuits / éléments du LLM qui capturent certains concepts, avec des circuits identifiés par approches d’observation de l’espace latent (ACP sur les états cachés du LLM à différents niveaux du réseau), de dictionnary learning pour visualiser quels concepts sont capturés par chaque neurones / groupes de neurones, ou par “patching”, en modifiant certains états cachés pour voir l’effet sur le modèle.
- Celles étudiant la génération des modèles (ou "generation" dans l'image), notamment des modèles dits de "raisonnement" (thinking) qui détaillent leur raisonnement dans la réponse qu'ils fournissent : cette approche est d’autant plus utile aujourd’hui que les agents consistent en plusieurs appels du LLMs (un appel qui retourne un appel à un outil (tool), un autre qui retourne l’appel à un autre outil, etc).
Nous allons d'abord observer les approches d'explicabilité par les données, que ce soit par les données d'entraînement ou par les données d'input (du prompt). L’objectif est d’établir des liens causaux clairs entre ces sources de données et les tokens générés, qu’ils soient pris individuellement ou en groupes de tokens.
I/ Approches TDA (training data attribution) pour comprendre quelles connaissances apprises dans l’entraînement ont été influentes dans la génération de quels tokens




1. Les fonctions d’influence pour estimer l’impact d’un exemple d’entraînement sur la prédiction d’un exemple de test
Si on cherche à estimer l’impact qu'aurait un exemple d'entraînement sur la perte d'un exemple de test (ou sur plusieurs résultats du modèle sur un jeu de données test) à un exemple d'entraînement (qu’il soit dans le jeu de données d’entraînement de base ou pas), on peut utiliser les fonctions d’influence.
\[\mathrm{Influence}\bigl(z_{\mathrm{train}}\to z_{\mathrm{test}}\bigr) = \frac{d}{d\varepsilon}\, \mathcal{L}\bigl(z_{\rm test},\,\theta_\varepsilon(z_\text{train})\bigr)\Big|_{\varepsilon=0} = -\nabla_\theta \,\mathcal{L}\bigl(z_{\mathrm{test}},\,\hat{\theta} \bigr)\,H_\theta^{-1}(\hat{\theta})\,\nabla_\theta \mathcal{L}(z_{\rm train},\hat{\theta})\] \[\mathrm{Influence}\bigl(z_{\mathrm{train}}\to f(x)\bigr) = \left.\frac{d}{d\varepsilon}\bigl(f_{\theta_{\varepsilon}(z_{\mathrm{train}})}(x)\bigr)\right|_{\varepsilon=0} = - \nabla_\theta f_{\hat{\theta}}(x)^\top \, H_\theta(\hat{\theta})^{-1} \, \nabla_\theta \mathcal{L}\bigl(x_{\mathrm{train}},\hat{\theta}\bigr)\]Pour voir l’explication de la formule et plus de détails sur comment c’est utilisé dans les LLMs, vous pouvez aller voir ce post.
La librairie Kronfluence permet de calculer l’influence dans le cas des LLMs. Des repo github proposent des tutos pour plusieurs de libs de calcul de l’influence dans les modèles de deep learning, comme Influenciae (btw, c’est une lib d’un labo de Toulouse!). Les fonctions d’influence permettent de répondre à ce genre de questions:
- Est-ce que je devrais ajouter cet exemple dans mon set d'apprentissage pour améliorer les performances de cette prédiction?
- Quels exemples d'entraînement ont été utiles à la prédiction de mon modèle?
- Le modèle s’est trompé: sur quels exemples d’entraînement s’est-il basé pour cette mauvaise prédiction?
2. Les approches d’attribution aux données d’entraînement par similarité sémantique
Pour trouver les données d’entraînement influentes pour la génération du LLM, on peut également simplement étudier la similarité sémantique entre la génération du LLM et les données d’entraînement.
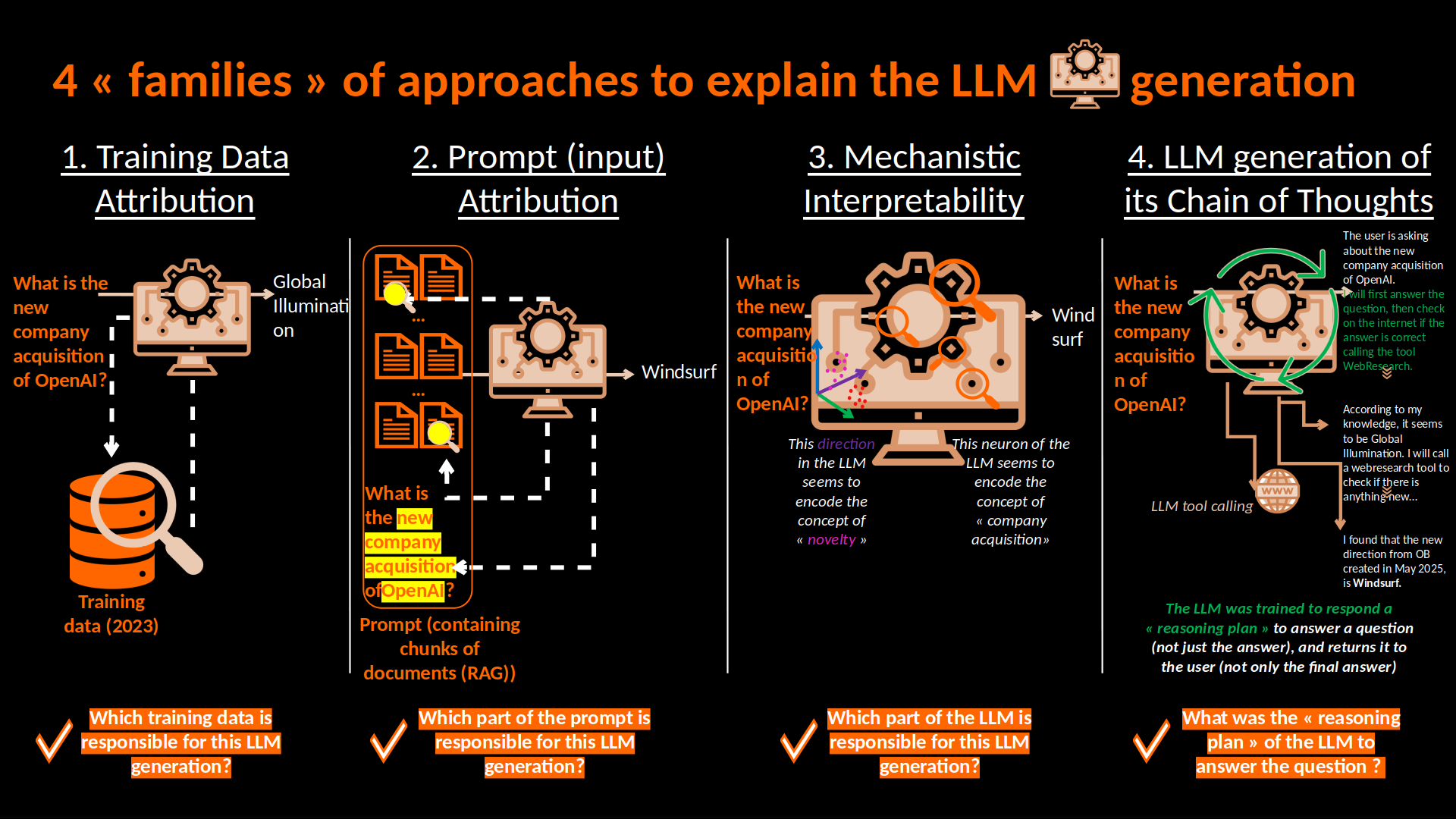
Le papier Wrapper Boxes: Faithful Attribution of Model Predictions to Training Data compare l’embedding de la génération du LLM à celui de la penultième couche, et entraîne ensuite trois types de « wrapper boxes » sur ces embeddings:
- un k-nearest neighbors (kNN) pour retrouver, à chaque inférence, les k exemples d’entraînement les plus proches ;
- un clustering k-means pour assigner l’input à un cluster dont on peut exposer le centroïde et les exemples qui le composent ;
- un arbre de décision dont chaque feuille correspond à un sous-ensemble d’exemples d’entraînement utilisés pour la classification.
Cliquez pour voir l’illustration de Wrapper Boxes
3. Les approches d’attribution aux données d’entraînement basées sur le gradient
Ces approches sont ressemblantes mais différentes des fonctions d'influence classiques, qu'on a vu plus tôt. En effet, ces fonctions d’influence calculent comment la perte sur un échantillon test, ou comment une fonction du modèle sur un échantillon donné changerait si on retirait / up-weightait un échantillon d’entraînement. Ici, les approches basées sur le gradient utilisent une notion plus simple: on calcule la distance entre 2 gradients: celui de la loss sur l’échantillon d’entraînement dont on veut voir l’influence avec celui de la loss sur l’exemple cible sur lequel on veut mesurer l’influence. Il y a plusieurs façons de calculer la distance entre les gradients: par produit scalaire, distance cosinus, …
Le papier Detecting and Filtering Unsafe Training Data via Data Attribution identifie les données d’entraînement “unsafe” à l’aide d’une distance cosinus entre les gradients d’un exemple “unsafe” et des exemples du jeu d’entraînement:
\[\begin{split} \text{DABUF-inf}(z_\text{train}, z\text{target}) &= \eta \cdot \cos(\nabla L(z_\text{target}; \theta), \nabla L(z_\text{train}; \theta)) \\ &= \eta \cdot \frac{\nabla L(z_\text{target}; \theta) \cdot \nabla L(z_\text{train}; \theta)}{||\nabla L(z_\text{target}; \theta)|| \cdot ||\nabla L(z_\text{train}; \theta)||} \end{split}\]On a aussi TracIn, qui lui ne calcule pas la distance cosinus entre les gradient mais effectue un produit scalaire entre eux.
4. Les approches d’attribution aux données d’entraînement basées sur les valeurs de Shapley
les valeurs de shapley estiment l’effet moyen de sous-ensembles d’un dataset en supprimant certaines variables explicatives (ici, certains datapoints du dataset) et en mesurant la différence de prédiction du modèle, puis en moyennant ces effets marginaux sur toutes les permutations possibles.
L’utilisation des valeurs de Shapley pour déterminer la contribution de datapoints à la prédiction du modèle peut être vue comme une évaluation des contributions marginales Beta Shapley: a Unified and Noise-reduced Data Valuation Framework for Machine Learning. La contribution marginale d’un point de données $z_i$ à un sous-ensemble de taille $k$ de l’ensemble d’entraînement est définie comme:
\[\Delta^{D_N}_{z_i}(k, D_T) := \frac{1}{\binom{n-1}{k}} \sum_{\substack{S \subseteq N \setminus \{i\} \\ |S|=k}} \bigl(U(S\cup\{i\},D_T) - U(S,D_T)\bigr).\]L’approche Leave-one-out (cf fonctions d’influences plus haut) considère la variation de la précision du modèle lorsqu’on retire le point cible de l’ensemble d’entraînement. Cette LOO peut être interprétée comme la contribution marginale de $z_i$ à $D_N\setminus{z_i}$. Les approches “leave-one-out” ou ses approximations (comme les fonctions d’influence, cf plus haut), ne considèrent que la contribution marginale de $z_i$ à un unique sous-ensemble de taille $n-1$ (avec $n$ étant la taille du jeu d’entraînement du modèle). Ainsi, le score d’instance d’un exemple chute fortement lorsqu’un autre exemple similaire apparaît dans l’ensemble d’entraînement (cf papier Data Shapley: Equitable Valuation of Data for Machine Learning), ce qui réduit la fiabilité et la robustesse de la mesure.
Au lieu de ne considérer qu’un sous-ensemble, la valeur de Shapley la généralise en tenant compte de l’impact de $z_i$ sur tous les sous-ensembles. En gros, au lieu de considérer: \(g^{\mathrm{LOO}}(z_i, D_T, D_N) = \Delta^{D_N}_{z_i}(n-1, D_T).\) On considère: \(g^{\mathrm{Shap}}(z_i, D_T, D_N) = n^{-1} \sum_{k=0}^{n-1} \Delta^{D_N}_{z_i}(k, D_T).\) Ceci peut être vu comme la moyenne des contributions marginales de $z_i$ à des sous-ensembles de toutes tailles possibles.
Cependant, calculer la valeur de Shapley sur un ensemble d’entraînement de taille $n$ exige un nombre exponentiel d’ajustements du modèle (soit $n!$), ce qui nécessite ajustements lorsque les datasets sont très grands (comme pour les LLMs).
Le papier Helpful or Harmful Data? Fine-tuning-free Shapley Attribution for Explaining Language Model Predictions propose une méthode d’attribution aux données d’entraînement basée sur les valeurs de Shapley, appelée FreeShap (Fine-tuning-free Shapley Attribution), basée sur la théorie du noyau tangent neuronal (NTK) pour éviter de multiples réentraînements du modèle.
En effet, la théorie du noyau tangent neuronal (NTK) a été proposée pour étudier la dynamique d’entraînement des réseaux de neurone. Les travaux On Exact Computation with an Infinitely Wide Neural Net et Toward a theory of optimization for over-parameterized systems of non-linear equations: the lessons of deep learning montrent que l’entraînement d’un réseau entièrement suffisamment large est équivalent à la résolution d’une régression par noyau avec le NTK à l’initialisation aléatoire. Cependant, deux défis se posent lorsque l’on applique la théorie NTK au fine-tuning des LMs : (1) l’utilisation quasi systématique de poids préentraînés au lieu d’une initialisation aléatoire ; (2) l’emploi de prompts. Le papier de 2023 A Kernel-Based View of Language Model Fine-Tuning étend l’analyse pour montrer que résoudre la régression par noyau avec le NTK empirique (eNTK) calculé à partir des poids préentraînés peut reproduire le fine-tuning basé sur des prompts. De plus, la régression par noyau utilisant l’eNTK obtient des performances comparables au fine-tuning en computer vision (cf le papier More Than a Toy: Random Matrix Models Predict How Real-World Neural Representations Generalize) et en NLP (cf papier A Kernel-Based View of Language Model Fine-Tuning), ce qui en fait un substitut prometteur.
L’eNTK se calcule à partir du Jacobien de la sortie du modèle pour un point de données $x_i$ : \(\psi(x_i)\;:=\;\frac{\partial f(x_i;\theta_0)}{\partial \theta_0} \;\in\;\mathbb{R}^{C\times P},\) où $\theta_0\in\mathbb{R}^P$ désigne les poids préentraînés.
Pour un ensemble d’entraînement $D_S$ d’indices $S:={1,\dots,k}$, on pose \(X_S \;:=\; \begin{bmatrix}x_1 \\ \vdots \\ x_k\end{bmatrix} \in\mathbb{R}^{k\times d}, \quad Y_S \;:=\; \begin{bmatrix} y^1_1 & \cdots & y^C_1 \\ \vdots & & \vdots \\ y^1_k & \cdots & y^C_k \end{bmatrix} \;\in\;\{0,1\}^{k\times C},\) où $y^p_j=1$ si la classe réelle de $x_j$ est $p$.
Une instance de test $x_t$ est alors prédite par le modèle de régression eNTK : \(f_S^{\mathrm{eNTK}}(x_t) \;=\; K(x_t, X_S)^\top \,K(X_S, X_S)^{-1}\, Y_S, \tag{5}\) avec \(K(x_t, X_S) =\bigl[\psi(x_t)\,\psi(x_i)^\top\bigr]_{i=1}^k \;\in\;\mathbb{R}^{C\times k}, \quad K(X_S, X_S) =\bigl[\psi(x_i)\,\psi(x_j)^\top\bigr]_{i,j=1}^k \;\in\;\mathbb{R}^{kC\times kC}.\)
II/ Approche Input (prompt) attribution: mesurer sur quelles parties de l’input le modèle s’est basé pour faire sa prédiction
Ces approches consistent à attributer la génération du LLM à des tokens du prompt pour comprendre quel(s) token(s) est/sont responsable(s) de quelle(s) parties de la génération du LLM.
Dans ce papier: A Close Look at Decomposition-based XAI-Methods for Transformer Language Models, 2025, ils comparent plusieurs approches (qu’on va détailler ci-dessous) de context / input attribution:
Cliquez la comparaison des tokens du prompts influents sur la génération du LLM par différentes approches comme présentées dans le papier




1. Les approches basées sur l’attention
Ces approches affichent les poids d’attention de chaque token générés par rapport aux tokens du prompt (cas auto-regressif). Des poids d’attention élevés signifient que le modèle a donné plus d’importance à ce token pour la génération du token en question.
Cependant, les poids d’attention sont donnés dans le réseau au niveau de chaque tête d’attention. Il est compliqué d’obtenir une attention “globale” que le modèle donne aux tokens. En effet, les scores d’attention ne montrent que les connexions locales (au sein de chaque tête de chaque couche du réseau), et surtout, ces patterns d’attention ne donnent tel quel aucune information : il s’agit de patterns uniformes. Plusieurs approches visent donc à modéliser ce flux d’attention global à travers le réseau pour tracer l’influence de chaque token d’entrée sur les tokens prédits.
Tout l’enjeu est d’arriver à mesurer, de manière la plus fidèle et informative possible, le flux d’attention au sein du réseau pour donner une vue globale de l’influence de chaque token d’entrée sur un token généré.
1.1 Visualisation du LLM comme un graphe d’attentions pour obtenir la contribution finale du token
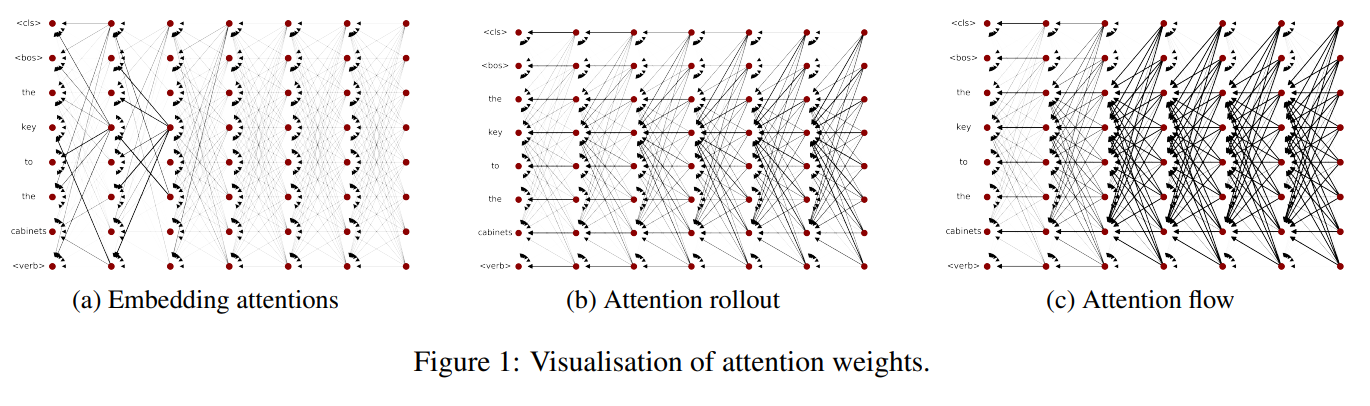
Le papier Quantifying Attention Flow in Transformers propose deux approches: une d’attention rollout et une d’attention flow. Ces 2 approches modélisent le LLM comme un graphe d’attention et utilisent chacune une méthode différente pour calculer l’attention globale d’un token sur le token prédit.
La première approche proposée est dite d’“attention rollout”. Elle consiste à multiplier récursivement les matrices d’attention à travers toutes les couches. L’idée est de représenter le LLM comme un graphe d’attentions: Si chaque arête représente la proportion d’information transférée, multiplier les poids le long d’un chemin donne le flux total.
La seconde approche est dite d’“attention flow”, avec dans l’idée de traiter le graphe d’attention comme un réseau de flux (flow network). Il utilise un algorithme de flux maximum où les capacités des arêtes sont les poids d’attention. Dans cette approche, le poids d’un chemin est le minimum des poids (pas le produit).
Cliquez pour voir l’illustration des poids d'attention selon ces 2 méthodes
1.2 La contribution globale d’un token associée aux logits au sein des différents blocs d’attention (et MLP)
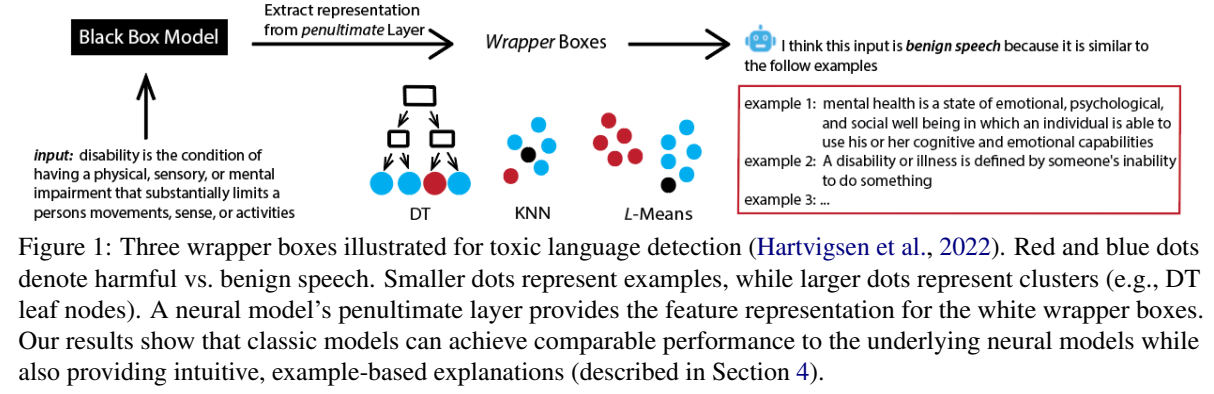
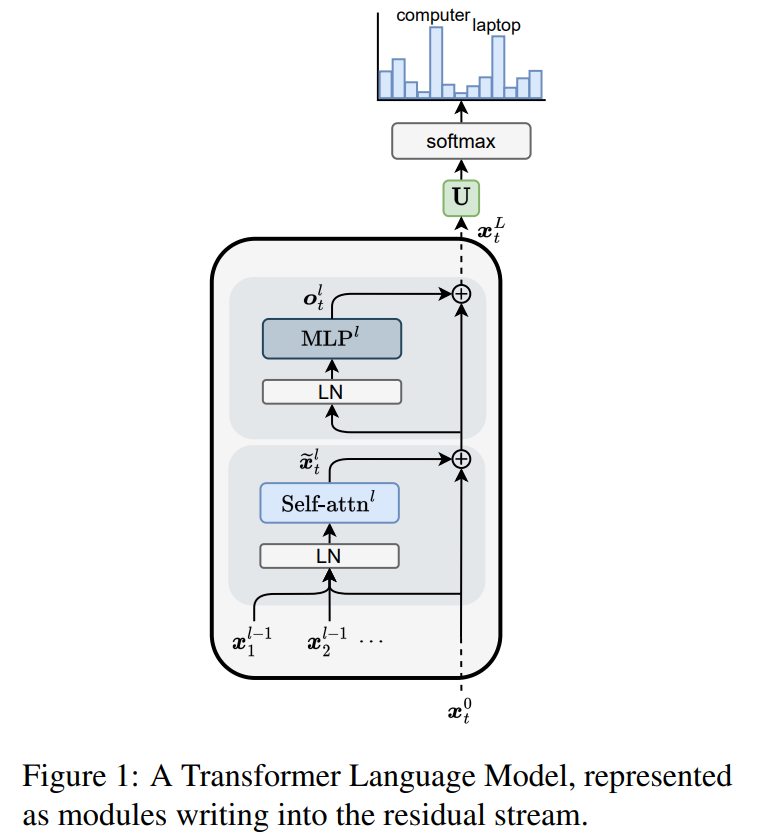
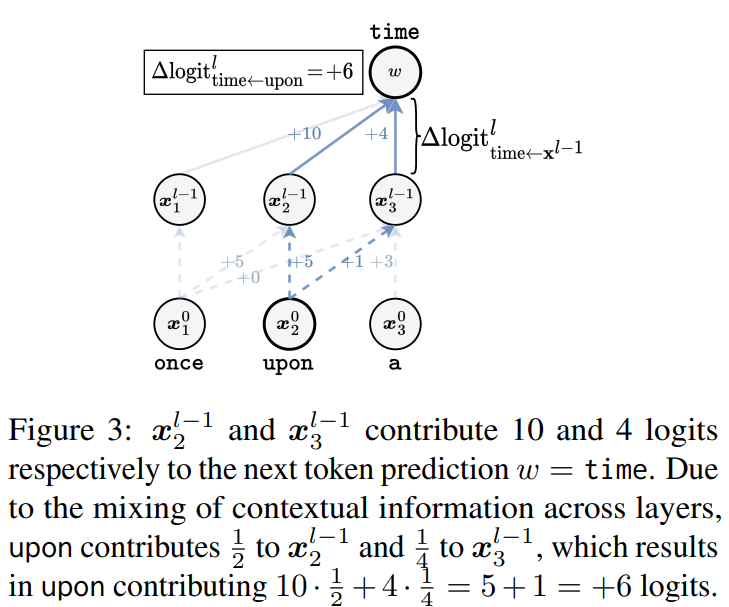
ALTI-Logit Explaining How Transformers Use Context to Build Predictions suit comment chaque token d’entrée contribue à la prédiction finale en traversant le réseau, en prenant en compte la contribution de chaque élément au logit, ainsi que l’ensemble des transformations (notamment au niveau du MLP) réalisées sur les scores d’attention pour évaluer cette contribution. En gros, pour calculer la contribution finale d’un token, ALTI-logit trace comment ce token (au logit du mot évalué) se propage à travers les connexions d’attention et les connexions résiduelles de toutes les couches, en tenant compte du mélange d’information entre tokens à chaque étape.
Cliquez pour voir l’illustration la composition d'un block transformers
Pour chaque couche $l$ : \(\begin{aligned} \Delta_{\mathrm{MLP}}^l &= \mathrm{sortie}^l_{\mathrm{MLP}} \;-\; \mathrm{entrée}^l_{\mathrm{MLP}},\\ \mathrm{relevance}_{\mathrm{MLP}}^l &= \Delta_{\mathrm{MLP}}^l \;\cdot\; U_w, \end{aligned}\) où $U_w$ est le vecteur d’unembedding de sortie pour le token suivant.
\textbf{Exemple (couche 10)} : \(\begin{aligned} \mathrm{entrée}_{\mathrm{MLP}}^{10} &= [0.1,\;0.2,\;\dots],& \mathrm{sortie}_{\mathrm{MLP}}^{10} &= [0.3,\;0.5,\;\dots],\\ \Delta_{\mathrm{MLP}}^{10} &= [0.2,\;0.3,\;\dots],& \Delta_{\mathrm{MLP}}^{10} \cdot \mathrm{embedding}_{\text{dort}} &= 1.5. \end{aligned}\)
Cliquez pour voir l’illustration de ALTI-logit
1.3 Visualisation de l’attention (sa propagation dans le réseau) comme un graphe à plusieurs niveaux
On peut voir l’attention comme un graphe à plusieurs niveaux: en effet, il y a d’abord les tokens (premier niveau, groupe A) sur lequels le token prédit par le LLM porte son attention. Mais il y a ensuite les tokens sur lesquels les tokens du groupe A portent leur attention (second niveau, groupe B), et ainsi dessuite. On peut remonter ainsi l’attention à plusieurs niveaux.
Afin d’identifier comment les tokens du prompt sont traitées par le LLM dans ses différentes têtes d’attention pour amener à l’output, le papier Fine-Tuning Enhances Existing Mechanisms: A Case Study on Entity Tracking teste d’abord toutes les têtes d’attention pour voir lesquelles, quand patchées (modification par une version bruitée de la tête d’attention: ici obtenue à l’aide de 2 fine-tuning différents: l’un bruité et l’autre d’origine), affectent le plus le logit final. Les têtes qui causent la plus grande chute de performance sont celles qui “regardent” directement la réponse correcte (Ces têtes forment le Groupe A). Le papier cherche ensuite quelles têtes d’attention ont un effet direct important sur les têtes du Groupe A, en patchant les chemins allant de candidats potentiels vers le Groupe A.
Cliquez pour voir l’illustration de l'approche de la propagation de l'attention par groupes
Le papier On the Emergence of Position Bias in Transformers représente en effet le masque d’attention comme un graphe $G$ dirigé où:
- Les nœuds représentent les tokens de la séquence
- une arrête $(j,i) \in E(G)$ signifie que l’attention du token $i$ est portée sur le token $j$
La propagation de l’information au sein des différentes couches du réseau se fait comme cela:
Pour une couche unique: \(X^{(1)} = A^{(0)}X^{(0)}W_V^{(0)}\), Pour 2 couches: \(X^{(2)} = A^{(1)}A^{(0)}X^{(0)}W_V^{(0)}W_V^{(1)}\) Pour t couches: \(X^{(t+1)}_{i,:} = \sum_{j=1}^{N} \underbrace{(A^{(t)} \cdots A^{(0)})_{ij}}_{P^{(t)}(z_i=j|X^{(0)})} \cdot \underbrace{X^{(0)}_{j,:} W_V^{(0)} \cdots W_V^{(t)}}_{f^{(t)}(X^{(0)}_{z_i,:})}\)
Le produit cumulatif $P^{(t)} = A^{(t)} \cdots A^{(0)}$ représente la probabilité cumulative que le token $i$ sélectionne le token $j$ comme contexte après $t$ couches. Cela capture tous les chemins possibles de longueur $t+1$ entre les tokens $j$ et $i$ dans le graphe.
Le papier Chain and Causal Attention for Efficient Entity Tracking généralise ce pattern d’attention “multi-niveau” en proposant un nouveau mécanisme d’attention qui, en une seule couche, permet toutes les connexions d’attention précédemment faites entre les couches. Pour cela, il utilise une représentation formelle avec le produit cumulatif des matrices d’attention qui permet de capturer toutes les longueurs de chemins en une seule couche. En effet, le papier interprète la matrice d’attention $A$ comme une matrice d’adjacence d’un graphe dirigé pour capturer toutes les dépendances possibles : \(A + A^2 + A^3 + \cdots = A(I - A)^{-1}\), avec $A$ connexions directes (chemins de longueur 1), $A^2$ chemins de longueur 2, $A^3$ chemins de longueur 3, etc. L’attention qu’ils proposent est calculée comme :
\[\boxed{Y = (1 - \gamma) \cdot A(I - \gamma A)^{-1}V}\]où $\gamma \in [0, 1)$ est un hyperparamètre qui assure la convergence de la série $A + \gamma A^2 + \gamma^2 A^3 + \cdots$ et permet l’interpolation entre attention standard ($\gamma = 0$) et ChaCAL ($\gamma \approx 1$).
1.4 Intérêt des approches basées sur l’attention: “facilement” manipulables pour “forcer” le modèle à porter / ne pas porter son attention sur certains tokens
Le papier Tell Your Model Where to Attend: Post-hoc Attention Steering for LLMs force l’attention du LLM vers des parties spécifiques du prompt désignées par l’utilisateur, à la manière dont nous utilisons le gras ou l’italique dans les textes humains pour diriger l’attention du lecteur.
Cliquez pour voir l’illustration de l'approche PASTA
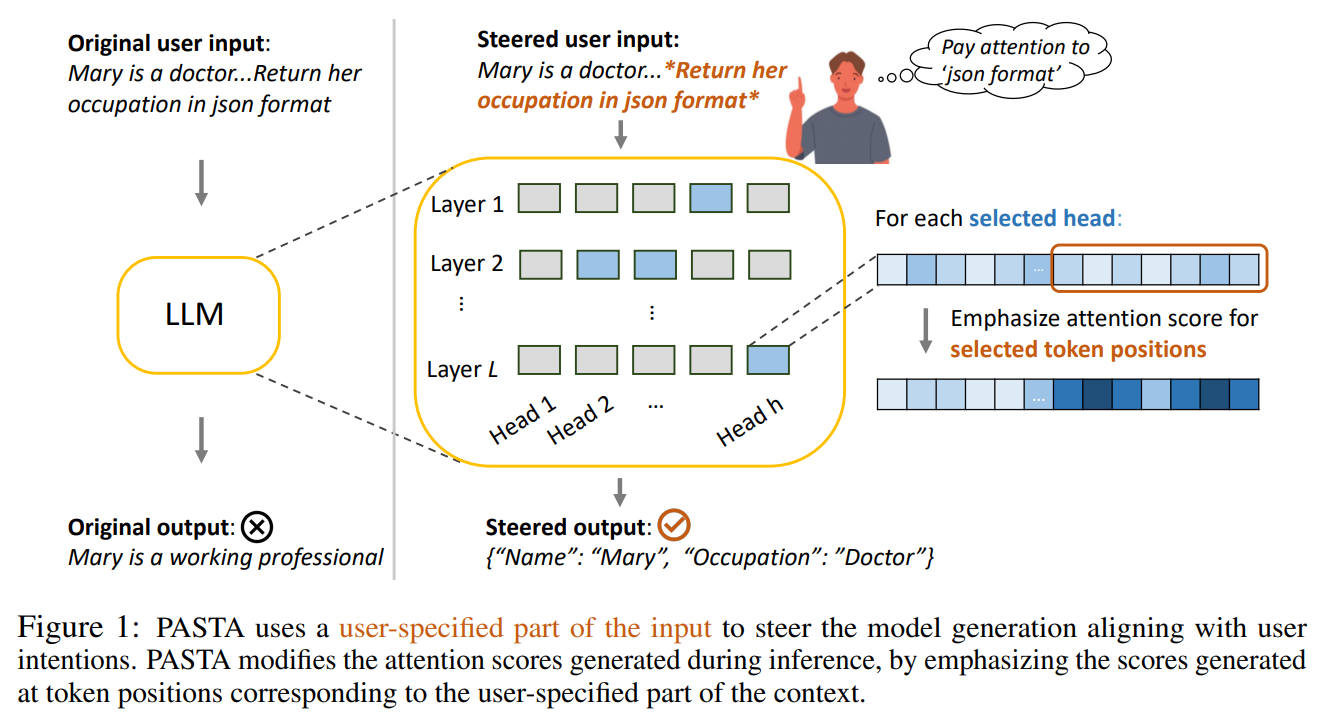
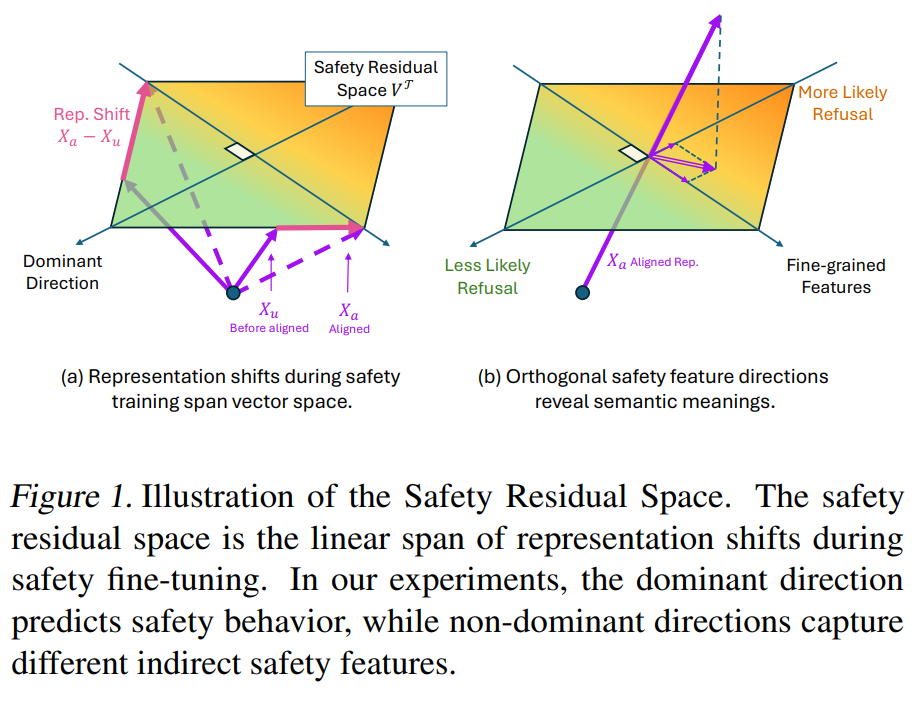
Le papier The Hidden Dimensions of LLM Alignment: A Multi-Dimensional Analysis of Orthogonal Safety Directions propose une approche plus complexe, pour neutraliser l’attention sur les tokens déclencheurs de jailbreak, qu’il identifie en exploitant la structure multi-dimensionnelle de l’espace résiduel de sécurité, construit comme la transformation linéaire des activations pendant le safety fine-tuning. Les tokens déclencheurs sont identifiés non pas par une seule direction, mais par l’interaction entre une direction dominante qui prédit le comportement de refus global, et plusieurs directions non-dominantes qui capturent des patterns spécifiques de jailbreak. Ces directions sont extraites via SVD de la matrice représentant les changements d’activation.
Cliquez pour voir l’illustration du papier du "safety residual space"
Cependant, ces approches basées sur l’attention pour mesurer l’importance d’un token du prompt sur la génération du modèle sont limitéesn puisque même si le modèle porte une attention plus forte à un token donné, cela ne veut pas nécessairement dire que ce token exerce une influence plus importante sur les logits. C’est pour ça que les apprioches basées sur le gradient ont plus de sens pour mesurer l’impact des tokens du prompt sur la génération du modèle:
2. Approches basées sur le gradient: les cartes de saillance (saliency maps)
Ces approches mesurent comment la sortie du modèle $f(x)$ varie si on modifie chaque token $x_i$ de l’entrée.
Plus précisément, les tokens étant représentés par des embeddings de dimension $d_{\text{model}}$, on calcule le gradient de $f(x)$ par rapport à chaque dimension de l'embedding de chaque token $x_i$. On obtient donc, pour chaque token, un vecteur gradient de dimension $d_{\text{model}}$. Pour obtenir un score de saillance scalaire par token, on agrège ces $d_{\text{model}}$ gradients à l'aide de différentes méthodes :
- Norme L2 : $|\nabla_{x_i} f(x)|_2$
- Norme L1 (somme des valeurs absolues) : $|\nabla_{x_i} f(x)|_1$
- Produit scalaire avec l’embedding : $\nabla_{x_i} f(x) \cdot x_i$
Pour se faire, des libraires comme Captum ou Inseq ou Grad-cam ou Investigate ou Alibi existent.
J’ai créé un repo github qui reproduit un papier (MIRAGE) d’explication de la génération du modèle à partir des éléments du prompt, découpés document par document (cas du RAG).
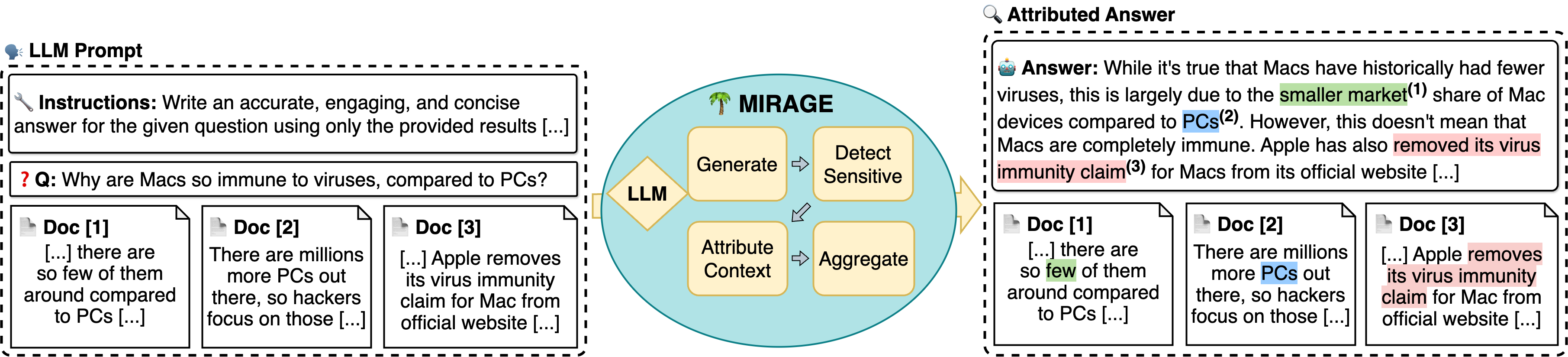
Ici, on parle d’attribution de l’importance des tokens du prompt dans la génération du LLM par calcul de gradient, c’est à dire simplement en dérivant la sortie du LLM par rapport aux tokens du prompt. Le problème, c’est que quand la fonction est localement plate (gradient nul), l’attribution est nulle même si l’input est important. L’approche des gradients intégrés (IG) (introduits dans le papier Axiomatic Attribution for Deep Networks), résout ces problèmes en intégrant les gradients le long d’un chemin entre une baseline neutre et l’input réel.
Soit $x = (x_1, x_2, …, x_n)$ le vecteur d’embeddings correspondant aux tokens du prompt, et $x’ = (x’_1, x’_2, …, x’_n)$ une baseline neutre (typiquement des embeddings nuls ou des tokens de padding). Pour un modèle $F$ produisant une sortie $y = F(x)$, l’importance du $i$-ème token est calculée par :
\[IG_i(x) = (x_i - x'_i) \times \int_{\alpha=0}^{1} \frac{\partial F(x' + \alpha \times (x - x'))}{\partial x_i} d\alpha\]Cette formule capture l’accumulation des gradients lorsqu’on interpole linéairement entre la baseline $x’$ et l’entrée réelle $x$. Le terme $(x_i - x’_i)$ représente la différence entre l’embedding du token réel et celui de la baseline, tandis que l’intégrale accumule les sensibilités du modèle tout au long du chemin d’interpolation.
En pratique, l’intégrale est approximée par une somme de Riemann (cas discret) :
\[IG_i(x) \approx (x_i - x'_i) \times \sum_{k=1}^{m} \frac{\partial F(x' + \frac{k}{m} \times (x - x'))}{\partial x_i} \times \frac{1}{m}\]où $m$ est le nombre de pas d’intégration. Cette méthode garantit deux propriétés importantes : la sensibilité (un token n’ayant aucun impact aura une attribution nulle) et la complétude (la somme des attributions égale la différence entre les sorties du modèle pour l’entrée réelle et la baseline).
Le papier Barkan et al., Improving LLM Attributions with Randomized Path-Integration, 2024 améliore la méthode des gradients intégrés (IG) en introduisant de la randomisation dans le processus d’intégration pour générer de meilleures attributions. En effet, contrairement à IG qui intègre les gradients par rapport aux embeddings d’entrée, RPI intègre les gradients par rapport aux scores d’attention du modèle. Ainsi, pour chaque couche, il calcule les gradients de la prédiction par rapport au tenseur d’attention interpolé le long d’un chemin randomisé entre une baseline aléatoire et les scores d’attention réels.
3. Approches basées sur les vecteurs: décomposition des représentations intermédiaires faites par le LLM de chaque token du prompt avec ACP
Une autre approche consiste à étudier l’espace latent (c’est à dire les représentations intermédiaires (à différents niveaux du réseau) du LLM) des tokens d’entrée pour étudier cet espace : comment une perturbation de cet espace modifie la génération du LLM? Comment est structuré cet espace? Est-ce qu’en modifiant / étudiant les directions de cet espace je peux en déduire quelque chose sur la sortie du LLM?
Le papier How do Language Models Bind Entities in Context? par exemple utilise des perturbations sur les représentations intermédiaires des tokens du prompt pour voir leur impact sur la génération du LLM.
Cliquez pour voir l’illustration du papier binding ids, perturbant les représentations intermédiaires des tokens du prompt pour voir l'impact sur la génération du LLM
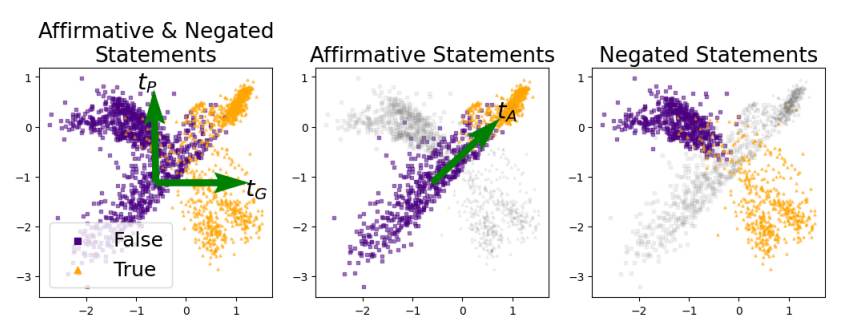
Le papier Truth is Universal: Robust Detection of Lies in LLMs effectue quand à lui une ACP sur les représentations intermédiaires du dernier token de chaque phrase (le “.”) - le modèle étudié étant autorégressif, le dernier token encode la globalité de la phrase. Ils effectuent cette ACP sur les représentations intermédiaires d’un ensemble de données comprenant des phrases vraies (triangles orange dans les figures) et fausses (carrés violets), qu’ils avaient annotées au préalable. Ils observent deux directions principales qui émergent de cette analyse : une direction “générale de vérité” (tG) qui sépare efficacement les déclarations vraies des fausses indépendamment de leur polarité (affirmative ou négative), et une direction “sensible à la polarité” (tP) qui distingue les phrases affirmatives des phrases négatives. Dans l’espace d’activation du modèle, tG pointe systématiquement des déclarations fausses vers les vraies, indépendamment de la polarité grammaticale (affirmative/négative). On peut donc prédire si la génération du LLM va être une hallucination ou non à l’aide de cet espace.
Cliquez pour voir l’illustration du papier qui fait l'ACP sur les représentations intermédiaires d'un ensemble de prompts vrai et faux
III/ Les approches d’explicabilité mécanistique (inférence): comprendre quelle partie du LLM est responsable de quel concept

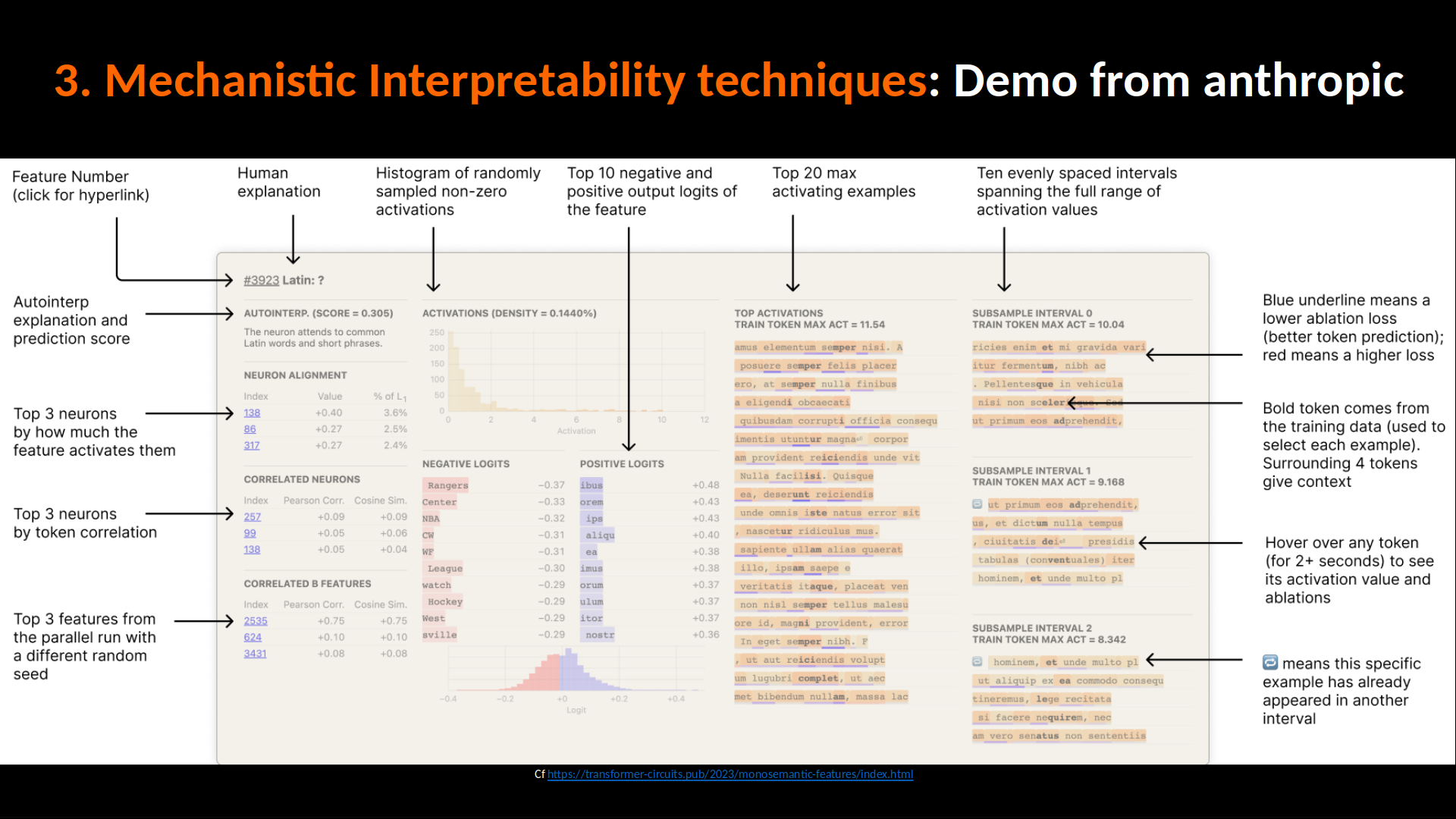

Le papier Open Problems in Mechanistic Interpretability décrit tous les défis / enjeux d’explicabilité mécanistique.
1. Les sondes sur l’espace latent
Ces approches consistent à étudier l’espace latent du modèle en lui donnant différents concepts en entrée (les “sondes”).
1.1 Les approches de sonde par ablation de l’espace latent
L’ablation de l’espace latent consiste à une mise à zéro ou suppression d’une activation.
- Ablation de couches, têtes d’attention ou paramètres
- Localisation de composants responsables :
- Hallucinations : Jin et al. (2024), Li et al. (2024a)
- Jailbreaks : Zhao et al. (2024d), Wei et al. (2024)
- Biais : Yang et al. (2023b), Ma et al. (2023)
1.2 Les approches de sonde par patching de l’espace latent
Le patching consiste à remplacer une activation par une autre.
- Inspiré de l’analyse de médiation causale (Pearl, 2001)
- Remplacement d’activations intermédiaires
- Applications : Hallucinations (Monea et al., 2024), biais (Vig et al., 2020)
Pour étudier les circuits:
- Path patching : Wang et al. (2023), Goldowsky-Dill et al. (2023)
1.3 Les approches de sonde par observation (réduction de dimension et autre) de l’espace latent
Il s’agit de projections de l’espace latent calculé sur différents concepts. On affiche donc les représentations des tokens / phrases avec et sans un concept spécifique, pour essayer de trouver un élément de l’espace latent qui les sépare.
Pour se faire, on peut effectuer une moyenne des vecteurs appartenant à un certain concept (hallucinations (Liu et al., On the Universal Truthfulness Hyperplane Inside LLMs, 2024), jailbreaks (Arditi et al. Refusal in Language Models Is Mediated by a Single Direction, 2024)), ou encore des méthodes de réduction de dimension de l’espace latent, comme l’ACP (Duan et al., Do LLMs Know about Hallucination? An Empirical Investigation of LLM’s Hidden States). D’autres approches entraînent un classifier sur les représentations de l’espace latent (Détection d’hallucinations Burns et al., Discovering Latent Knowledge in Language Models Without Supervision, 2022, Truth is Universal: Robust Detection of Lies in LLMs, Bürger et al., 2024, jailbreaks Zhou et al., How Alignment and Jailbreak Work: Explain LLM Safety through Intermediate Hidden States, 2024).
Cependant, ces différents approches supposent que ces concepts sont encodés comme directions linéaires, alors que ce n’est pas vraiment le cas dans les LLMs.
1.4 Ces approches permettent de “corriger” le modèle en dirigeant d’une certaine manière les vecteurs latents
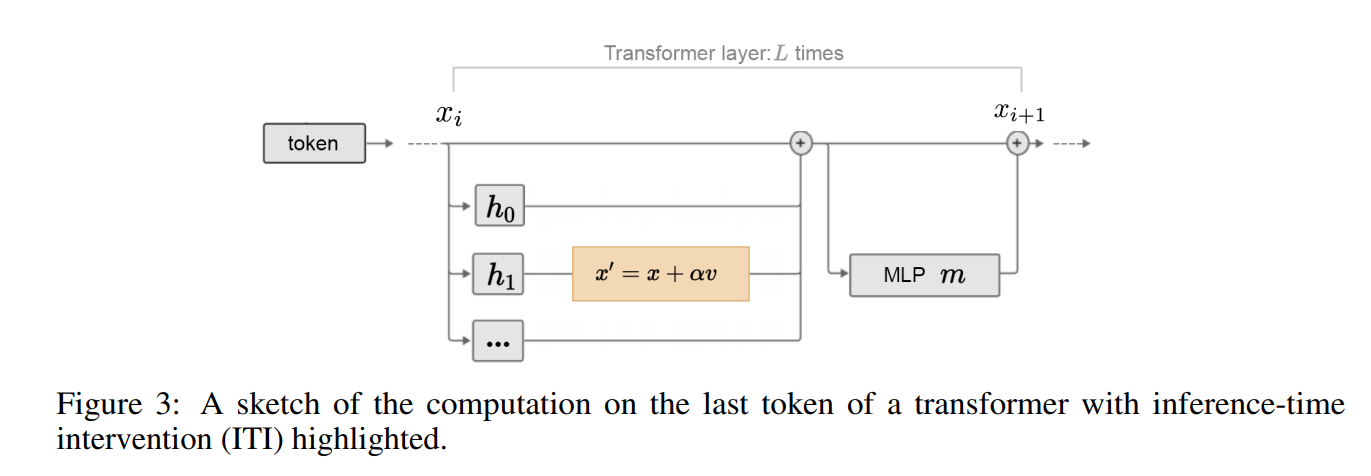
cf: hallucinations Li et al., Inference-Time Intervention: Eliciting Truthful Answers from a Language Model, 2023, jailbreaks Turner et al.,Steering Language Models With Activation Engineering, 2023
Exemple des figures de ces papiers pour “corriger” le modèle selon ces direction:
Le papier Inference-Time Intervention: Eliciting Truthful Answers from a Language Model propose cette approche:
Cliquez pour voir l’illustration de l'intervention sur les activations du modèle
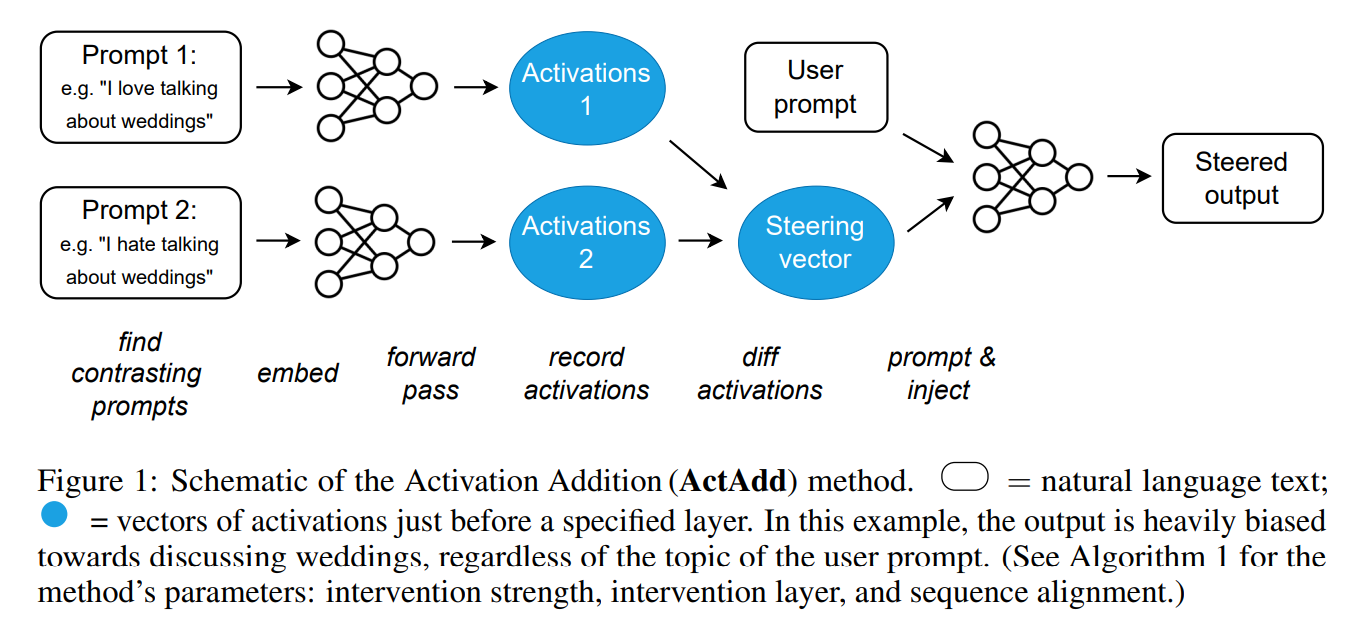
Le papier Steering Language Models With Activation Engineering propose cette approche:
Cliquez pour voir une autre illustration d'une intervention sur les activations du modèle
Le papier Refusal in Language Models Is Mediated by a Single Direction qui corrige les poids du modèle de la direction $r$ identifiée comme générant des jailbreaks : $x’ = x - rr^Tx$. L’ablation directionnelle « met à zéro » la composante suivant $r$ pour chaque activation du flux résiduel $x \in \mathbb{R}^{d_{\text{model}}}$.
1.2 Les auto-encodeurs pour apprendre un “dictionnaire” des éléments du réseau (Sparse Dictionnary Learning)
Analyse des neurones individuels
Autoencodeurs épars (SAE)
- Objectif : Désentrelement des concepts superposés
- Architecture : Encodeur → vecteur épars de concepts → Décodeur
- Références clés :
- Fondamentaux : Sharkey et al. (2022), Bricken et al. (2023)
- Améliorations : Rajamanoharan et al. (2024a), Templeton et al. (2024)
- Applications sécurité :
- Hallucinations : Ferrando et al. (2025), Theodorus et al. (2025)
- Jailbreaks : Härle et al. (2024), Muhamed et al. (2025)
- Biais : Hegde (2024), Zhou et al. (2025a)
Logit lens
- Projection des vecteurs latents intermédiaires sur l’espace vocabulaire
- Origine : nostalgebraist (2020), Elhage et al. (2021)
- Améliorations : Belrose et al. (2023), Din et al. (2023)
- Applications : Mécanismes de stockage/rappel (Yu et al., 2023), hallucinations (Yu et al., 2024b)
1.2.1 Le principe de superposition : Analyse des neurones individuels
Selon l’hypothèse de superposition, un réseau peut représenter plus de caractéristiques qu’il n’a de dimensions, à condition que chaque feature s’active de manière parcimonieuse. (chaque caractéristique (feature) d’un réseau de neurones ne doit pas être activée tout le temps, mais seulement dans des cas spécifiques et rares)
Ces approches de SDL sont plus sophistiquées et “state of the art” que les approches de réduction de dimension avec ACP ou autre des activations, justement dû au fait de la polysémanticité des neurones. Si un neurone encode à la fois : “nature”, “vieux”, “lumière” dans un même sous-espace de représentation, l’ACP ne pourra pas dissocier ces trois concepts si leurs activations sont mélangées dans les mêmes dimensions.
En gros, les activations sont traitées par un petit réseau neuronal à deux couches, correspondant respectivement à un encodeur et un décodeur, avec un espace latent large: L’encodeur encode l’activation de chaque variable latente, et le décodeur est une matrice qui sert de dictionnaire des directions latentes.

- Identification des entrées activant fortement un neurone
- Références : Geva et al. (2021), Foote et al. (2023)
- Défi : Polysémantique des neurones (Arora et al., 2018)
- Fondamentaux : Sharkey et al. (2022), Bricken et al. (2023)
- Améliorations : Rajamanoharan et al. (2024a), Templeton et al. (2024)
- Hallucinations : Ferrando et al. (2025), Theodorus et al. (2025)
- Jailbreaks : Härle et al. (2024), Muhamed et al. (2025)
- Biais : Hegde (2024), Zhou et al. (2025a)
Il existe plusieurs approches de SDL, qui traitent des activations différentes:
- Les autoencodeurs parcimonieux (SAE) (classique)
- Les transcodeurs (cf papier Transcoders Find Interpretable LLM Feature Circuits)
- Les crosscodeurs (cf article Sparse Crosscoders for Cross-Layer Features and Model Diffing)
1.2.2 Analyse de groupes de neurones à différents niveaux dans le réseau
Les concepts sont ici représentées non par par neurone mais sur plusieurs layers. Du coup, il est naturel d’appliquer l’apprentissage de dictionnaires de manière conjointe entre les layers. Les crosscodeurs permettent de gérer la persistance d’une feature sur plusieurs couches.
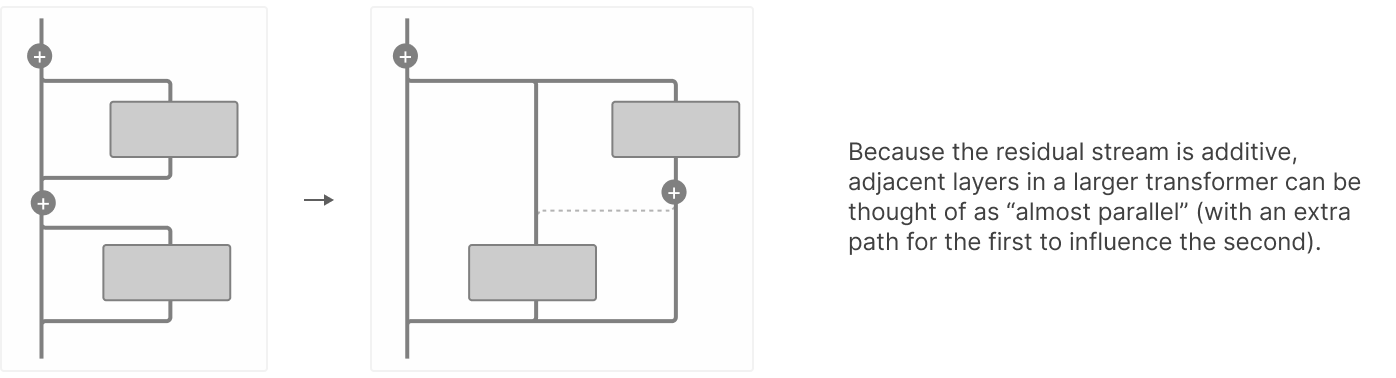
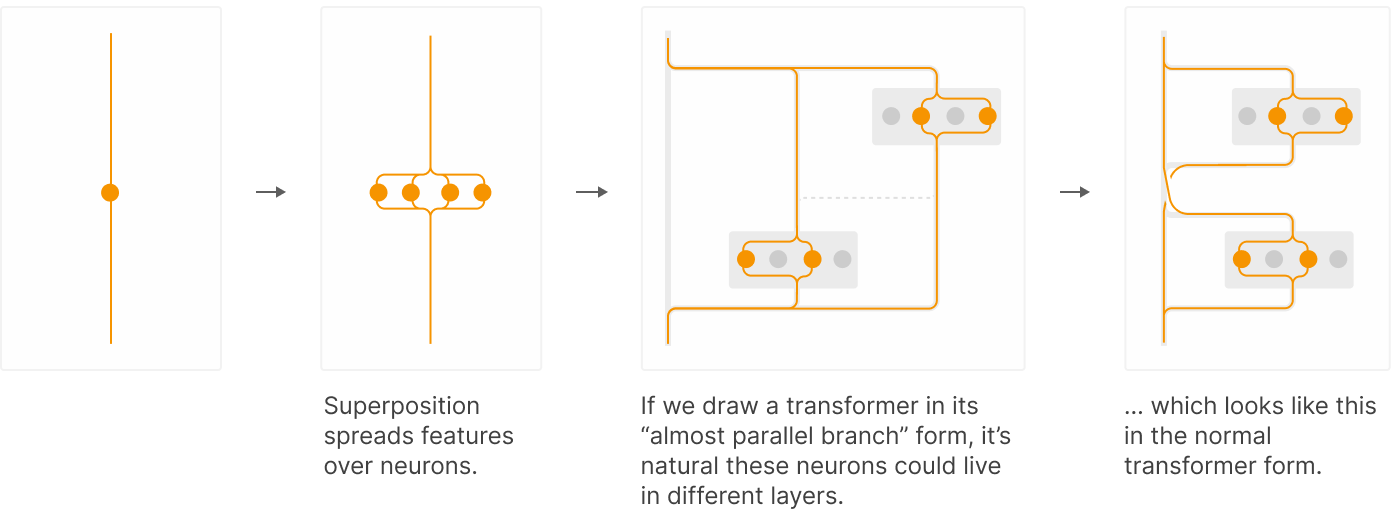
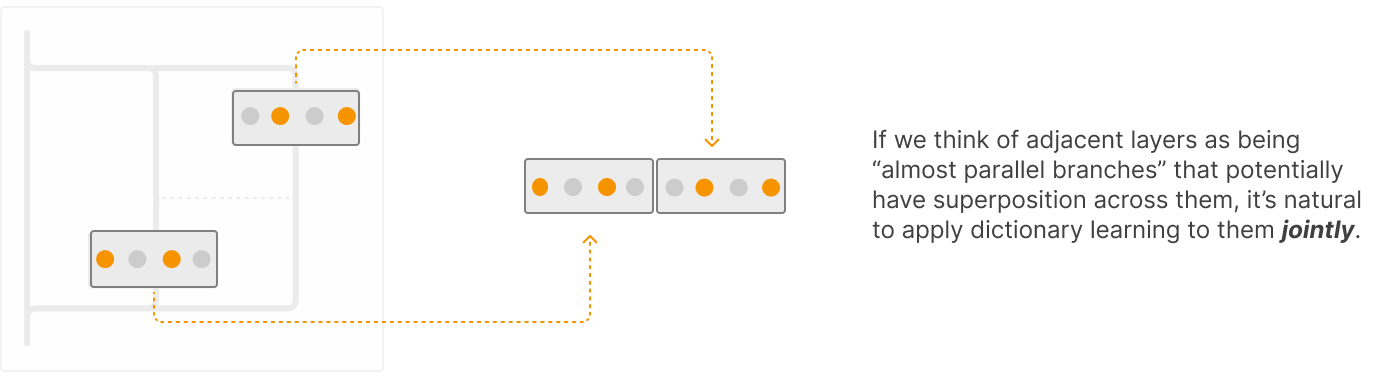
Les crosscodeurs peuvent nous aider en cas de superposition entre couches, mais ils peuvent également être utiles lorsqu’une feature calculée reste dans le flux résiduel pendant de nombreuses couches. Considérons le cycle de vie hypothétique suivant d’une feature à travers le flux résiduel :

IV/ Les approches d’explicabilité par Génération de Raisonnement du LLM


Explorer comment les LLM peuvent interpréter leurs propres sorties en exprimant le raisonnement sous-jacent.
Raisonnement en génération
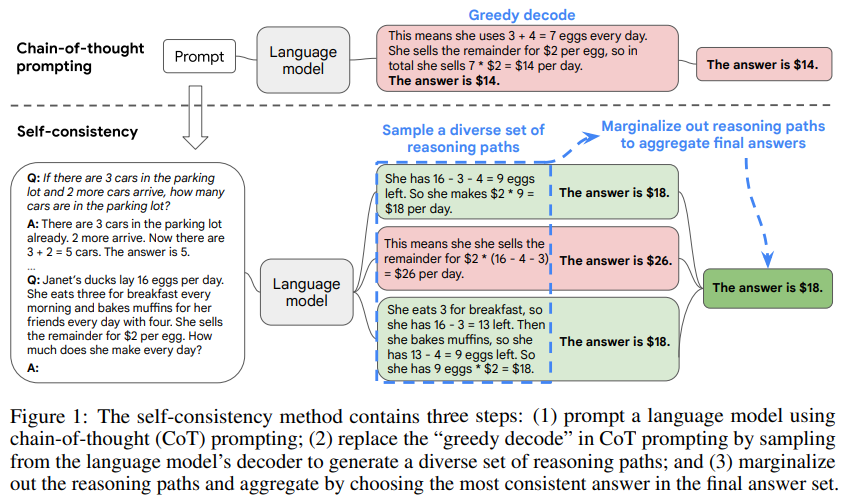
Chain-of-Thought (CoT)
La Chain of Thought consiste à fournir, dans le prompt, quelques exemples de raisonnements détaillés pas-à-pas (“intermediate steps”), incitant le modèle à « penser à voix haute » avant de donner sa réponse.
Plusieurs approches “améliorées” du CoT ont émergées:
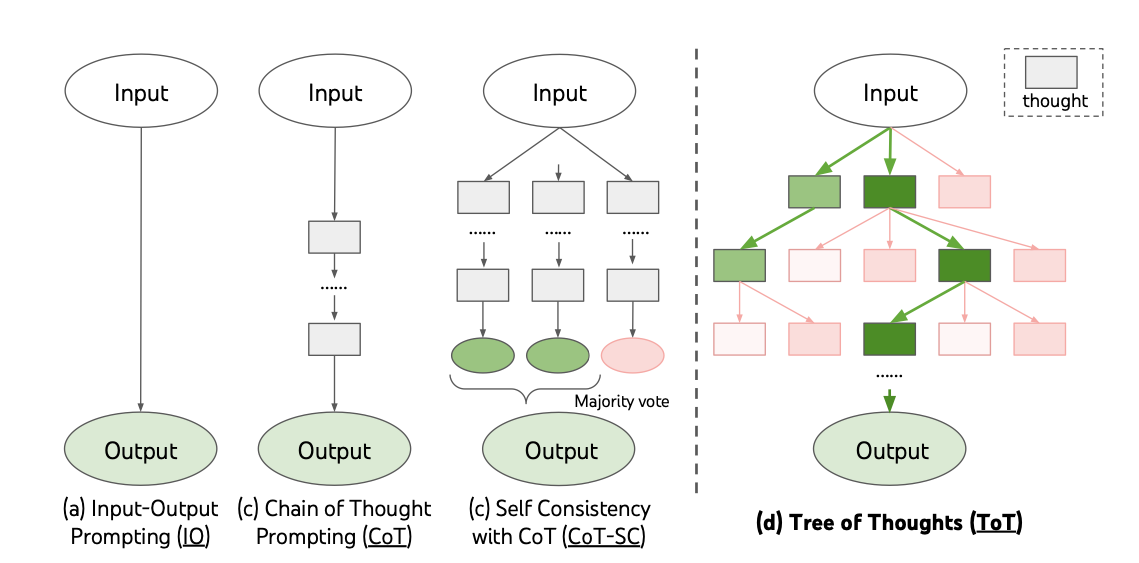
Il y a notamment le CoT-SC (Chain of Thought Self Consistency) qui consiste à choisir la réponse la plus fréquente ou la plus cohérente en agrégeant ces chemins de raisonnement issu du CoT, comme présenté dans le papier Self-Consistency Improves Chain of Thought Reasoning in Language Models
Cliquez pour voir une illustration du CoT-SC
Extension via le Tree of Thoughts (ToT)
Tree of Thoughts étend la CoT en explorant un arbre de pensées : à chaque nœud, le modèle génère plusieurs « thoughts » candidates, peut les évalue globalement, … Tree of Thoughts: Deliberate Problem Solving with Large Language Models
Combinaison du CoT et de l’appel de tool des LLMs (cas des agents) : ReAct
Le paradigme ReAct combine raisonnement (traces de CoT) et actions (interrogation d’API, interaction avec un environnement) de façon intercalée, permettant de corriger en temps réel et de réduire l’hallucination.
ReAct: Synergizing Reasoning and Acting in Language Models
Autres papiers sur le sujet
Quelques papiers intéressants sur le sujet: Advancing Reasoning in Large Language Models: Promising Methods and Approaches From System 1 to System 2: A Survey of Reasoning Large Language Models A Survey on Latent Reasoning Reasoning Beyond Language: A Comprehensive Survey on Latent Chain-of-Thought Reasoning